
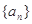 的前n項和記為
的前n項和記為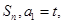 點
點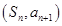 在直線
在直線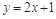 上,
上,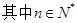 .(1)若數(shù)列
.(1)若數(shù)列 是等比數(shù)列,求實數(shù)
是等比數(shù)列,求實數(shù)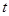 的值;
的值;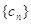 中,所有滿足
中,所有滿足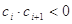 的整數(shù)
的整數(shù)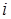 的個數(shù)稱為這個數(shù)列
的個數(shù)稱為這個數(shù)列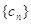 的“積異號數(shù)”,令
的“積異號數(shù)”,令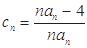 (
(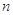
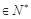 ),在(1)的條件下,求數(shù)列
),在(1)的條件下,求數(shù)列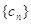 的“積異號數(shù)”
的“積異號數(shù)” ,化簡得an+1=3an(n≥2),要使n≥1時{an}是等比數(shù)列,只需
,化簡得an+1=3an(n≥2),要使n≥1時{an}是等比數(shù)列,只需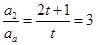 ,從而得出t的值.
,從而得出t的值.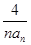 =
=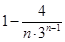 ,計算可得c1c2=-1<0,再由cn+1-cn>0可得,數(shù)列{cn}遞增,由c2=
,計算可得c1c2=-1<0,再由cn+1-cn>0可得,數(shù)列{cn}遞增,由c2=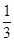 >0,得當n≥2時,cn>0,由此求得數(shù)列{cn}的“積異號數(shù)”為1.
>0,得當n≥2時,cn>0,由此求得數(shù)列{cn}的“積異號數(shù)”為1.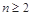 時,有
時,有
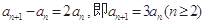 , 3分
, 3分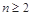 時
時 是等比數(shù)列,要使
是等比數(shù)列,要使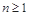 時
時 是等比數(shù)列,則只需
是等比數(shù)列,則只需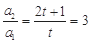
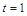 5分
5分 的首項為
的首項為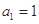 ,公比
,公比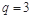 ,∴
,∴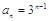
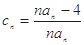
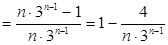 7分
7分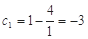 ,
,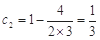 ,∴
,∴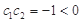
 ,
,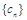 遞增. 10分
遞增. 10分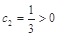 ,得當
,得當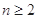 時,
時,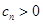 .
.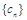 的“積異號數(shù)”為1. 12分
的“積異號數(shù)”為1. 12分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
| A.150 | B.135 | C.125 | D.100 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 是公比大于1的等比數(shù)列,
是公比大于1的等比數(shù)列, 為數(shù)列
為數(shù)列 的前
的前 項和,已知
項和,已知 ,且
,且 構(gòu)成等差數(shù)列.
構(gòu)成等差數(shù)列. 的通項公式;
的通項公式; ,求數(shù)列
,求數(shù)列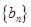 的前
的前 項的和
項的和 .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題

查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
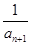 -
-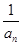 =d(n∈N*,d為常數(shù)),則稱數(shù)列{an}為“調(diào)和數(shù)列”.已知正項數(shù)列{
=d(n∈N*,d為常數(shù)),則稱數(shù)列{an}為“調(diào)和數(shù)列”.已知正項數(shù)列{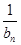 }為“調(diào)和數(shù)列”,且b1+b2+…+b9=90,則b4·b6的最大值是( )
}為“調(diào)和數(shù)列”,且b1+b2+…+b9=90,則b4·b6的最大值是( )| A.10 | B.100 | C.200 | D.400 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
 ,
, ,
, ,
, ,…為梯形數(shù).根據(jù)圖形的構(gòu)成,記此數(shù)列的第
,…為梯形數(shù).根據(jù)圖形的構(gòu)成,記此數(shù)列的第 項為
項為 ,則
,則 ( )
( )
A. | B. | C. | D. |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com