
(Ⅰ)求證OD∥平面PAB;
(Ⅱ)當k=![]() 時,求直線PA與平面PBC所成角的大小;
時,求直線PA與平面PBC所成角的大小;
(Ⅲ) 當k取何值時,O在平面PBC內(nèi)的射影恰好為△PBC的重心?
18.解:方法一:
(Ⅰ)∵O、D分別為AC、PC的中點,
∴OD∥PA

又PA![]() 平面PAB,
平面PAB,
∴OD∥平面PAB
(Ⅱ)∵AB⊥BC,OA=OC
∴OA=OB=OC
又∴OP⊥平面ABC,
∴PA=PB=PC。
取BC中點E,連結(jié)PE,則BC⊥平面POE。
作OF⊥PE于F,連結(jié)DF,則OF⊥平面PBC。∠ODF是OD與平面PBC所成的角。
又OD∥PA,
∴PA與平面PBC所成角的大小等于∠ODF。
在Rt△ODF中,
sin∠ODF=![]() .
.
∴PA與平面PBC所成的角為arcsin![]() 。
。
(Ⅲ)由(Ⅱ)知,OF⊥平面PBC,
∴F是O在平面PBC內(nèi)的射影。
∵D是PC的中點
若點F是△PBC的重心。
則B、F、D三點共線,
∴直線OB在平面PBC內(nèi)的射影為直線BD。
∵OB⊥PC,
∴PC⊥BD,
∴PB=BC,即k=1
反之,當k=1時,三棱錐O-PBC為正三棱錐,
∴O在平面PBC內(nèi)的射影為△PBC的重心
方法二:
∵OP⊥平面ABC,OA=OC,AB=BC,
∴OA⊥OB,OA⊥OP,OB⊥OP。
以O(shè)為原點,射線OP為非負z軸,建立空間直角坐標系O-xyz(如圖),
設(shè)AB=a,則A(![]() a,0,0),B(0,
a,0,0),B(0,![]() a,0),C(-
a,0),C(-![]() a,0,0)。
a,0,0)。
設(shè)OP=h,則P(0,0,h)。

(Ⅰ)∵D為PC的中點,
∴![]() =(-
=(-![]() ,0,
,0,![]() )
)
又![]() ,
,
∴![]()
∴![]() ∥
∥![]() 。
。
∴OD∥平面PAB
(Ⅱ)∵k=![]() ,即PA=2a
,即PA=2a
∴h=![]() ,
,
∴![]() =(
=(![]() ),
),
可求得平面PBC的法向量![]() =(1,-1,-
=(1,-1,-![]() ),
),
∴cos<![]() ,
,![]() >=
>= =
=![]()
設(shè)PA與平面PBC所成的角為θ
則sinθ=|cos<![]() ,
,![]() >|=
>|=![]() ,
,
∴PA與平面PBC所成的角為arcsin![]()
(Ⅲ)△PBC的重心G(-![]() a,
a,![]() a,
a,![]() h),
h),
∴![]() =(-
=(-![]() a,
a,![]() a,
a,![]() h)
h)
∵OG⊥平面PBC,
∴![]() ⊥
⊥![]()
又![]() =(0,
=(0,![]() a,-h(huán))
a,-h(huán))
∴![]() ·
·![]() =
=![]() a2-
a2-![]() h2=0
h2=0
∴h=![]() a.
a.
∴PA=![]() =a,即k=1.
=a,即k=1.
反之,當k=1時,三棱錐O-PBC為正三棱錐,
∴O在平面PBC內(nèi)的射影為△PBC的重心。


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
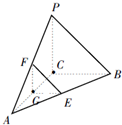 8、如圖,在三棱錐P-ABC中,已知PC⊥BC,PC⊥AC,點E,F(xiàn),G分別是所在棱的中點,則下面結(jié)論中錯誤的是( )
8、如圖,在三棱錐P-ABC中,已知PC⊥BC,PC⊥AC,點E,F(xiàn),G分別是所在棱的中點,則下面結(jié)論中錯誤的是( )查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
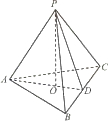 如圖,在三棱錐P-ABC中,AB=AC,D為BC的中點,PO⊥平面ABC,垂足O落在線段AD上,已知BC=8,PO=4,AO=3,OD=2
如圖,在三棱錐P-ABC中,AB=AC,D為BC的中點,PO⊥平面ABC,垂足O落在線段AD上,已知BC=8,PO=4,AO=3,OD=2查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
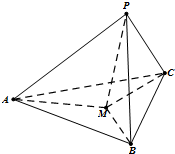 如圖,在三棱錐P-ABC中,PA,PB,PC兩兩垂直,且PA=5,PB=4,PC=3.設(shè)點M為底面ABC內(nèi)一點,定義f(M)=(m,n,p),其中m,n,p分別為三棱錐M-PAB、M-PBC、M-PCA的體積.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,則正實數(shù)a的取值范圍是
如圖,在三棱錐P-ABC中,PA,PB,PC兩兩垂直,且PA=5,PB=4,PC=3.設(shè)點M為底面ABC內(nèi)一點,定義f(M)=(m,n,p),其中m,n,p分別為三棱錐M-PAB、M-PBC、M-PCA的體積.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,則正實數(shù)a的取值范圍是查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
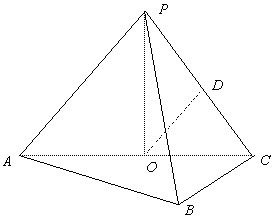
 如圖,在三棱錐P-ABC中,AB⊥BC,AB=BC=kPA,點O、D分別是AC、PC的中點,OP⊥底面ABC.
如圖,在三棱錐P-ABC中,AB⊥BC,AB=BC=kPA,點O、D分別是AC、PC的中點,OP⊥底面ABC.| 1 |
| 2 |
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
| z1+z2+z3 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2012•莆田模擬)如圖,在三棱錐P-ABC中,△PAC,△ABC分別是以A、B為直角頂點的等腰直角三角形,AB=1.
(2012•莆田模擬)如圖,在三棱錐P-ABC中,△PAC,△ABC分別是以A、B為直角頂點的等腰直角三角形,AB=1.| 3 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com