
【題目】某同學用“五點法”畫函數![]() 在某一個周期內的圖象時,列表并填入了部分數據,如下表:
在某一個周期內的圖象時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)請將上表數據補充完整;函數![]() 的解析式為
的解析式為![]() = (直接寫出結果即可);
= (直接寫出結果即可);
(2)求函數![]() 的單調遞增區間;
的單調遞增區間;
(3)求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
科目:高中數學 來源: 題型:
【題目】△ABC中,已知角A,B,C所對的邊分別為a,b,c, ![]() +
+ ![]() =
= ![]() ,b=4,且a>c.
,b=4,且a>c.
(1)求ac的值;
(2)若△ABC的面積為2 ![]() ,求a,c的值.
,求a,c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本著健康、低碳的生活理念,租自行車騎游的人越來越多.某自行車租車點的收費標準是每車每次租車時間不超過兩小時免費,超過兩小時的部分每小時收費2元(不足1小時的部分按1小時計算).有甲、乙兩人相互獨立來該租車點租車騎游(各租一車一次).設甲、乙不超過兩小時還車的概率分別為 ![]() ,
, ![]() ;兩小時以上且不超過三小時還車的概率分別為
;兩小時以上且不超過三小時還車的概率分別為 ![]() ,
, ![]() ;兩人租車時間都不會超過四小時. (Ⅰ)求甲乙兩人所付的租車費用相同的概率.
;兩人租車時間都不會超過四小時. (Ⅰ)求甲乙兩人所付的租車費用相同的概率.
(Ⅱ)設甲乙兩人所付的租車費用之和為隨機變量ξ,求ξ的分布列及數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() .
.
(Ⅰ)若a=1,求曲線y=f(x)在點(1,f(1))處的切線方程;
(Ⅱ)若函數f(x)在其定義域內為增函數,求a的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,設函數 ![]() ,若在[1,e]上至少存在一點x0 , 使得f(x0)≥g(x0)成立,求實數a的取值范圍.
,若在[1,e]上至少存在一點x0 , 使得f(x0)≥g(x0)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖:四棱錐P﹣ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,點M是CD的中點.
(1)求證:AM∥平面PBC;
(2)求證:CD⊥PA.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,AB為橢圓的一條弦(不經過原點),直線y=kx(k>0)經過弦AB的中點,與橢圓C交于P,Q兩點,設直線AB的斜率為k1 .
,AB為橢圓的一條弦(不經過原點),直線y=kx(k>0)經過弦AB的中點,與橢圓C交于P,Q兩點,設直線AB的斜率為k1 . 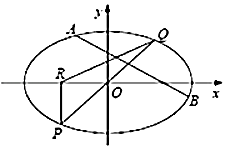
(1)若點Q的坐標為(1, ![]() ),求橢圓C的方程;
),求橢圓C的方程;
(2)求證:k1k為定值;
(3)過P點作x軸的垂線,垂足為R,若直線AB和直線QR傾斜角互補.若△PQR的面積為2 ![]() ,求橢圓C的方程.
,求橢圓C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在無窮數列![]() 中,
中, ![]() ,對于任意
,對于任意![]() ,都有
,都有![]() ,
, ![]() ,設
,設![]() ,記使得
,記使得![]() 成立的
成立的![]() 的最大值為
的最大值為![]() .
.
(![]() )設數列
)設數列![]() 為
為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,寫出
,寫出![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )若
)若![]() 為等比例數列,且
為等比例數列,且![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 為等差數列,求出所有可能的數列
為等差數列,求出所有可能的數列![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com