Question

已知＝(1,2)，＝(－2，n) (n>1)，與的夾角是45°.
(1)求；
(2)若與同向，且與－垂直，求.

Answer 1

(1)＝(－2,6)；(2)＝(－1,3)；

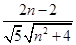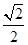解析試題分析：(1)由向量數量積的坐標表示得·＝2n－2，又由數量積公式可得cos 45°＝＝，所以可以求得；(2)由與－垂直得，(－)·＝0,又結合與同向，可設＝λ (λ>0)，帶入計算可得λ的值，λ算出后，即可得。
試題解析：解：(1)·＝2n－2，||＝，||＝，
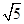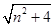∴cos 45°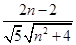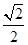＝＝，∴3n²－16n－12＝0，∴n＝6或n＝－ (舍)，∴＝(－2,6)．
(2)由(1)知，·＝10，||²＝5.又與同向，故可設＝λ (λ>0)，(－)·＝0，
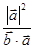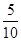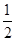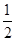
∴λ·－||²＝0，∴λ＝＝＝，∴＝＝(－1,3)．
考點：1、向量的坐標運算及數量積；2、向量垂直的坐標運算；