【題目】已知橢圓
，
，
，
，
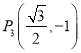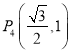四點中恰有三點在橢圓
上，拋物線
焦點到準線的距離為
.
（1）求橢圓、拋物線
的方程；
（2）過橢圓右頂點Q的直線
與拋物線交于點A、B，射線
、
分別交橢圓于點
、
.
（i）證明：
為定值；
（ii）記
、
的面積分別為
、
，求
的最小值.
應用題天天練四川大學出版社系列答案科目：高中數學 來源： 題型：
【題目】有以下命題：
①存在實數
，
，使得
；
②“
，
”的否定是“存在
，
”；
③擲一枚質地均勻的正方體骰子，向上的點數不小于3的概率為
；
④在閉區間
上取一個隨機數
，則
的概率為
．
其中所有的真命題為________．（填寫所有正確的結論序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解甲、乙兩種產品的質量，從中分別隨機抽取了10件樣品，測量產品中某種元素的含量（單位：毫克），如圖所示是測量數據的莖葉圖.規定：當產品中的此中元素的含量不小于18毫克時，該產品為優等品.
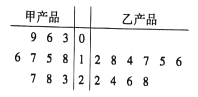
（1）試用樣品數據估計甲、乙兩種產品的優等品率；
（2）從乙產品抽取的10件樣品中隨機抽取3件，求抽到的3件樣品中優等品數
的分布列及其數學期望
；
（3）從甲產品抽取的10件樣品中有放回地隨機抽取3件，也從乙產品抽取的10件樣品中有放回地隨機抽取3件；抽到的優等品中，記“甲產品恰比乙產品多2件”為事件
，求事件的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】記焦點在同一條軸上且離心率相同的橢圓為“相似橢圓”.已知橢圓
，以橢圓
的焦點為頂點作相似橢圓
.
(Ⅰ)求橢圓的方程；
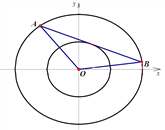
(Ⅱ)設直線
與橢圓交于
兩點，且與橢圓僅有一個公共點，試判斷
的面積是否為定值(
為坐標原點)？若是，求出該定值；若不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“新冠肺炎”疫情的控制需要根據大數據進行分析，并有針對性的采取措施.下圖是甲、乙兩個省份從2月7日到2月13日一周內的新增“新冠肺炎”確診人數的折線圖.根據圖中甲、乙兩省的數字特征進行比對，下列說法錯誤的是（ ）
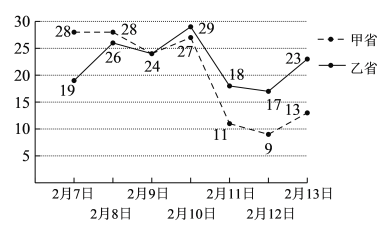
A.2月7日到2月13日甲省的平均新增“新冠肺炎”確診人數低于乙省
B.2月7日到2月13日甲省的單日新增“新冠肺炎”確診人數最大值小于乙省
C.2月7日到2月13日乙省相對甲省的新增“新冠甲省肺炎”確診人數的波動大
D.后四日（2月10日至13日）乙省每日新增“新冠肺炎”確診人數均比甲省多
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市9年前分別同時開始建設物流城和濕地公園，物流城3年建設完成，建成后若年投入x億元，該年產生的經濟凈效益為
億元；濕地公園4年建設完成，建成后的5年每年投入見散點圖．公園建成后若年投入x億元，該年產生的經濟凈效益為
億元．
（1）對濕地公園，請在
中選擇一個合適模型，求投入額x與投入年份n的回歸方程；
（2）從建設開始的第10年，若對物流城投入0.25億元，預測這一年物流城和濕地公園哪個產生的年經濟凈效益高？請說明理由．
參考數據及公式：
，
；當
時，
，
，回歸方程中的
；回歸方程
斜率與截距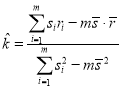
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
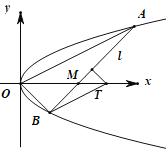
【題目】如圖，在平面直角坐標系
中，已知拋物線
，過點
的直線
交拋物線于
，
，
，
兩點.當
垂直于
軸時，
的面積為
.
0
（1）求拋物線的方程：
（2）設線段的垂直平分線交軸于點
.
①證明：
為定值：
②若
，求直線的斜率.
查看答案和解析>>
科目：高中數學 來源： 題型：
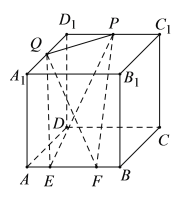
【題目】如圖，在長方體
中，
，
，
，
是棱
上的一條線段，且
，
是
的中點，
是棱
上的動點，則
①四面體
的體積為定值
②直線
到平面
的距離為定值
③點到直線的距離為定值
④直線
與平面
所成的角為定值
其中正確結論的編號是（ ）
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點A是以BC為直徑的圓O上異于B，C的動點，P為平面ABC外一點，且平面PBC⊥平面ABC，BC＝3，PB＝2
，PC
，則三棱錐P﹣ABC外接球的表面積為______．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
