【題目】南宋數學家楊輝在《詳解九章算法》和《算法通變本末》中，提出了一些新的垛積公式，所討論的高階等差數列與一般等差數列不同，前后兩項之差并不相等，但是逐項差數之差或者高次差成等差數列對這類高階等差數列的研究，在楊輝之后一般稱為“垛積術”.現有高階等差數列，其前7項分別為1，4，8，14，23，36，54，則該數列的第19項為（ ）（注：
）
A.1624B.1024C.1198D.1560
科目：高中數學 來源： 題型：
【題目】2019冠狀病毒病（CoronaVirus Disease2019（COVID-19））是由新型冠狀病毒（2019-nCoV）引發的疾病，目前全球感染者以百萬計，我國在黨中央、國務院、中央軍委的堅強領導下，已經率先控制住疫情，但目前疫情防控形勢依然嚴峻，湖北省中小學依然延期開學，所有學生按照停課不停學的要求，居家學習．小李同學在居家學習期間，從網上購買了一套高考數學沖刺模擬試卷，快遞員計劃在下午4：00～5：00之間送貨到小區門口的快遞柜中，小李同學父親參加防疫志愿服務，按規定，他換班回家的時間在下午4：30～5：00，則小李父親收到試卷無需等待的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，橢圓
的方程為
，且直線
與以原點為圓心，橢圓短軸長為直徑的圓相切．
（1）求
的值；
（2）若橢圓左右頂點分別為
，過點
作直線
與橢圓交于
兩點，且位于第一象限，
在線段
上．
①若
和
的面積分別為
，問是否存在這樣的直線使得
？請說明理由；
②直線
與直線
交于點，連結
，記直線的斜率分別為
，求證：
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某景點共有999級臺階，寓意長長久久.游客甲上臺階時，可以一步走一個臺階，也可以一步走兩個臺階，無其它可能.若甲每步上一個臺階的概率為
，每步上兩個臺階的概率也為.為了簡便描述問題，我們約定，甲從0級臺階開始向上走，一步走一個臺階記1分，一步走兩個臺階記2分，記甲登上第
個臺階的概率為
，其中
，且
.
（1）甲走3步時所得分數為
，求的分布列和數學期望；
（2）證明：當，且
時，數列
是等比數列，并求甲登上第100級臺階的概率
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,橢圓
：
的左、右焦點分別為
，橢圓上一點
與兩焦點構成的三角形的周長為6,離心率為
，
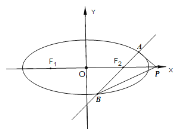
（Ⅰ）求橢圓的方程；
（Ⅱ）過點
的直線
交橢圓
于
兩點,問在
軸上是否存在定點,使得
為定值？證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某校運動會男生組田徑綜合賽以選手三項運動的綜合積分高低決定排名．具體積分規則如表1所示，某代表隊四名男生的模擬成績如表2．
表1 田徑綜合賽項目及積分規則
項目 | 積分規則 |
| 以 |
跳高 | 以 |
擲實心球 | 以 |
表2 某隊模擬成績明細
姓名 | 100米跑（秒） | 跳高（米） | 擲實心球（米） |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根據模擬成績，該代表隊應選派參賽的隊員是：（ ）
A.甲B.乙C.丙D.丁
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
