【題目】已知拋物線C：y2=2px（p＞0），其焦點為F（1，0），過F作斜率為k的直線交拋物線C于A、B兩點，交其準(zhǔn)線于P點．
（1）求P的值；
（2）設(shè)|PA|+|PB|=λ|PA||PB||PF|，若k∈[ 
，1]，求實數(shù)λ的取值范圍．
【答案】
（1）解：因為焦點F（1，0），所以 
，解得p=2．
（2）解：由題可知：直線AB的方程為y=k（x﹣1）（k≠0），準(zhǔn)線的方程為x=﹣1
設(shè)A（x1，y1），B（x2，y2），則 
．由 
消去y得k2x2﹣（2k2+4）x+k2=0，
故 
．
由|PA|+|PB|=λ|PA||PB||PF|得 
解得 
．
因為k∈[ 
，1]，所以λ∈[ ， 
]．
【解析】（1）運用拋物線的焦點坐標(biāo)，計算即可得到所求方程；（2）由題可知：直線AB的方程為y=k（x﹣1）（k≠0），準(zhǔn)線l的方程為x=﹣1，設(shè)A（x1 ， y1），B（x2 ， y2），聯(lián)立拋物線的方程，運用韋達(dá)定理和弦長公式，化簡整理，運用不等式的性質(zhì)，即可得到所求范圍．
名師指導(dǎo)期末沖刺卷系列答案
開心蛙口算題卡系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】若定義域為R的偶函數(shù)f（x）在[0，+∞）上是增函數(shù)，則不等式f（log4x）+f（log0.25x）≤2f（1）的解集為（ ）
A. [
，2] B. [
，4] C. [
，2] D. [
，4]
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知a=cos61°cos127°+cos29°cos37°， 
， 
，則a，b，c的大小關(guān)系是（ ）
A.a＜b＜c
B.a＞b＞c
C.c＞a＞b
D.a＜c＜b
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】動直線l：（3λ+1）x+（1﹣λ）y+6﹣6λ=0過定點P，則點P的坐標(biāo)為 ， 若直線l與x軸的正半軸有公共點，則λ的取值范圍是 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
；
（1）當(dāng)
時，若
，求
的取值范圍；
（2）若定義在
上奇函數(shù)
滿足
，且當(dāng)
時， 
，
求
在
上的反函數(shù)
；
（3）對于（2）中的
，若關(guān)于
的不等式
在
上恒成立，求實
數(shù)
的取值范圍；
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列函數(shù)中，在其定義域上既是奇函數(shù)又是增函數(shù)的是（ ）
A.y=logax
B.y=x3+x
C.y=3x
D.y=﹣ 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)f（x）= 
．
（1）求函數(shù)f（x）的定義域A；
（2）設(shè)B={x|﹣1＜x＜2}，當(dāng)實數(shù)a、b∈（B∩RA）時，證明： 
|．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
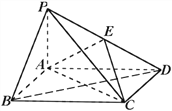
【題目】如圖，四棱錐
中，底面
為矩形， 
面
， 
為
的中點。
（1）證明： 
平面
;
（2）設(shè)
， 
，三棱錐
的體積 
，求A到平面PBC的距離。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
