
【題目】已知函數![]() 且a≠1,函數
且a≠1,函數![]() .
.
(1)判斷并證明f(x)和g(x)的奇偶性;
(2)求g(x)的值域;
(3)若x∈R,都有|f(x)|≥|g(x)|成立,求a的取值范圍.
【答案】(1)答案見解析.(2)![]() .(3)
.(3)![]() .
.
.
【解析】
(1)利用定義判斷函數的奇偶性得解;(2)利用雙勾函數的圖象和性質求出值域;(3)考慮到函數f(x),g(x)都是奇函數,故只需保證x≥0時都有|f(x)|≥|g(x)|即可,再對a分兩種情況a>1和0<a<1討論,利用導數求出實數a的取值范圍是![]() .
.
(1)首先,f(x),g(x)的定義域都是R,是關于原點對稱的,
其次,f(﹣x)=a﹣x﹣a﹣(﹣x)=﹣(ax﹣a﹣x)=﹣f(x),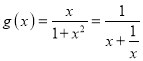 ,
,
∴函數f(x),g(x)均為奇函數;
(2)當x=0時,g(0)=0;
當x≠0時,![]() ,
,
令![]() ,則由雙勾函數的性質可知,t∈(﹣∞,﹣2]∪[2,+∞),
,則由雙勾函數的性質可知,t∈(﹣∞,﹣2]∪[2,+∞),
∴![]() ,即此時
,即此時![]() ,
,
綜上,函數g(x)的值域為![]() ;
;
(3)考慮到函數f(x),g(x)都是奇函數,故只需保證x≥0時都有|f(x)|≥|g(x)|即可,
這是因為當x<0時,|f(x)|=|f(﹣x)|,|g(x)|=|g(﹣x)|,
①先考慮a>1的情形,此時f(x)=ax﹣a﹣x≥1﹣1=0,g(x)≥0,
因此只需當x≥0時,f(x)﹣g(x)≥0恒成立即可,
令![]() ,則
,則![]() ,
,
令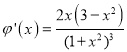 ,則
,則![]() ,
,
當![]() 時,φ′(x)>0,即φ(x)單增,故此時φ(x)min=φ(0)=﹣1;
時,φ′(x)>0,即φ(x)單增,故此時φ(x)min=φ(0)=﹣1;
當![]() 時,
時,![]() ,故x=0時,φ(x)氣的最小值﹣1,
,故x=0時,φ(x)氣的最小值﹣1,
若![]() ,則h′(x)=(ax+a﹣x)lna+φ(x)≥2lna﹣1≥0,
,則h′(x)=(ax+a﹣x)lna+φ(x)≥2lna﹣1≥0,
∴h(x)單增,故h(x)≥h(0)=0,符合題設;
若![]() ,則
,則 ,
,
且0<x<1時,![]() ,h′(x)單增,
,h′(x)單增,
故由零點存在性定理可知存在x0∈(0,1),使得h′(x0)=0,
且x∈(0,x0)時h′(x)<0,h(x)單減,當x∈(x0,1)時h′(x)>0,h(x)單增,
則h(x0)<h(0)=0,不符合題意,
故![]() ;
;
②再考慮0<a<1的情形,此時![]() ,
,
此時的![]() 與①中的a地位等價,同①理可知
與①中的a地位等價,同①理可知![]() ,即
,即![]() ,
,
綜合①②可知,實數a的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】某校為進行愛國主義教育,在全校組織了一次有關釣魚島歷史知識的競賽.現有甲、乙兩隊參加釣魚島知識競賽,每隊3人,規定每人回答一個問題,答對為本隊贏得1分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,且各人回答正確與否相互之間沒有影響,用ξ表示甲隊的總得分.
,且各人回答正確與否相互之間沒有影響,用ξ表示甲隊的總得分.
(Ⅰ)求隨機變量ξ的分布列和數學期望;
(Ⅱ)用![]() 表示“甲、乙兩個隊總得分之和等于3”這一事件,用
表示“甲、乙兩個隊總得分之和等于3”這一事件,用![]() 表示“甲隊總得分大于乙隊總得分” 這一事件,求
表示“甲隊總得分大于乙隊總得分” 這一事件,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如題所示的平面圖形中,![]() 為矩形,
為矩形,![]() ,
,![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 是以
是以![]() 為圓心,
為圓心,![]() 為直徑的半圓上任一點(不與
為直徑的半圓上任一點(不與![]() 重合),以
重合),以![]() 為折痕,將半圓所在平面
為折痕,將半圓所在平面![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如圖2,
,如圖2,![]() 為線段
為線段![]() 的中點.
的中點.
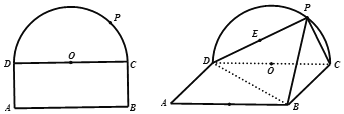
(1)證明:![]() .
.
(2)若銳二面角![]() 的大小為
的大小為![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出下列結論:
,給出下列結論:
(1)若對任意![]() ,且
,且![]() ,都有
,都有![]() ,則
,則![]() 為R上的減函數;
為R上的減函數;
(2)若![]() 為R上的偶函數,且在
為R上的偶函數,且在![]() 內是減函數,
內是減函數, ![]() (-2)=0,則
(-2)=0,則![]() >0解集為(-2,2);
>0解集為(-2,2);
(3)若![]() 為R上的奇函數,則
為R上的奇函數,則![]() 也是R上的奇函數;
也是R上的奇函數;
(4)t為常數,若對任意的![]() ,都有
,都有![]() 則
則![]() 關于
關于![]() 對稱。
對稱。
其中所有正確的結論序號為_________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com