
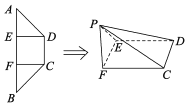
【題目】如圖所示,在等腰梯形ABCD中,![]() ,
,![]() ,E,F為AB的三等分點,且
,E,F為AB的三等分點,且![]() 將
將![]() 和
和![]() 分別沿DE、CF折起到A、B兩點重合,記為點P.
分別沿DE、CF折起到A、B兩點重合,記為點P.
![]() 證明:平面
證明:平面![]() 平面PEF;
平面PEF;
![]() 若
若![]() ,求PD與平面PFC所成角的正弦值.
,求PD與平面PFC所成角的正弦值.
【答案】(1)見解析;(2)![]()
【解析】
![]() 推導出四邊形CDEF是平行四邊形,
推導出四邊形CDEF是平行四邊形,![]() ,
,![]() ,
,![]() 由
由![]() ,得
,得![]() ,從而
,從而![]() 面PEF,由此能證明平面
面PEF,由此能證明平面![]() 平面PEF.
平面PEF.
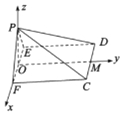
![]() 在平面PEF內作
在平面PEF內作![]() ,垂足為O,取CD的中點M,以O為坐標原點,建立空間直角坐標系
,垂足為O,取CD的中點M,以O為坐標原點,建立空間直角坐標系![]() ,利用向量法能求出PD與平面PFC所成角的正弦值.
,利用向量法能求出PD與平面PFC所成角的正弦值.
![]() ,
,![]() ,
,![]() 四邊形CDEF是平行四邊形,
四邊形CDEF是平行四邊形,![]() ,
,
![]() ≌
≌![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() 面PEF,
面PEF,
![]() 面PFC,
面PFC,![]() 平面
平面![]() 平面PEF.
平面PEF.
![]() 在平面PEF內作
在平面PEF內作![]() ,垂足為O,取CD的中點M,
,垂足為O,取CD的中點M,
由![]() 知
知![]() 平面PEF,故FC
平面PEF,故FC![]() ,
,![]() 平面CDEF,
平面CDEF,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,OF,OM兩兩垂直,
,OF,OM兩兩垂直,
以O為坐標原點,建立如圖所示的空間直角坐標系![]() ,
,
設![]() ,
,![]() 是等邊三角形,
是等邊三角形,
![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 2,
2,![]() ,
,![]() 2,
2,![]() ,
,
![]() 0,
0,![]() ,
,![]() 2,
2,![]() ,
,![]() 2,
2,![]() ,
,
設![]() y,
y,![]() 是平面PFC的法向量,
是平面PFC的法向量,
則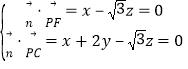 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
設PD與平面PFC所成角為![]() ,
,
則![]() ,
,
![]() 與平面PFC所成角的正弦值為
與平面PFC所成角的正弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】
已知點A(2,0),B(2,0),動點M(x,y)滿足直線AM與BM的斜率之積為![]() .記M的軌跡為曲線C.
.記M的軌跡為曲線C.
(1)求C的方程,并說明C是什么曲線;
(2)過坐標原點的直線交C于P,Q兩點,點P在第一象限,PE⊥x軸,垂足為E,連結QE并延長交C于點G.
(i)證明:![]() 是直角三角形;
是直角三角形;
(ii)求![]() 面積的最大值.
面積的最大值.
(二)選考題:共10分.請考生在第22、23題中任選一題作答。如果多做,則按所做的第一題計分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】當x∈[0,1]時,下列關于函數y=![]() 的圖象與
的圖象與![]() 的圖象交點個數說法正確的是( )
的圖象交點個數說法正確的是( )
A. 當![]() 時,有兩個交點B. 當
時,有兩個交點B. 當![]() 時,沒有交點
時,沒有交點
C. 當![]() 時,有且只有一個交點D. 當
時,有且只有一個交點D. 當![]() 時,有兩個交點
時,有兩個交點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列四個命題:
(1)“若![]() ,則
,則![]() ,
,![]() 互為倒數”的逆命題;
互為倒數”的逆命題;
(2)“面積相等的三角形全等”的否命題;
(3)“若![]() ,則
,則![]() 無實數解”的否命題;
無實數解”的否命題;
(4)命題:“空間中到一個正四面體的六條棱所在的直線距離均相等的點有且只有![]() 個”; 其中真命題( )
個”; 其中真命題( )
A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(1)(2)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產某種產品,一條流水線年產量為![]() 件,該生產線分為兩段,流水線第一段生產的半成品的質量指標會影響第二段生產成品的等級,具體見下表:
件,該生產線分為兩段,流水線第一段生產的半成品的質量指標會影響第二段生產成品的等級,具體見下表:
第一段生產的半成品質量指標 |
|
|
|
第二段生產的成品為一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生產的成品為二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生產的成品為三等品概率 | 0.5 | 0.3 | 0.1 |
從第一道生產工序抽樣調查了![]() 件,得到頻率分布直方圖如圖:
件,得到頻率分布直方圖如圖:

若生產一件一等品、二等品、三等品的利潤分別是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各組的中間值估計為該組半成品的質量指標,估算流水線第一段生產的半成品質量指標的平均值;
(Ⅱ)將頻率估計為概率,試估算一條流水線一年能為該公司創造的利潤;
(Ⅲ)現在市面上有一種設備可以安裝到流水線第一段,價格是![]() 萬元,使用壽命是
萬元,使用壽命是![]() 年,安裝這種設備后,流水線第一段半成品的質量指標服從正態分布
年,安裝這種設備后,流水線第一段半成品的質量指標服從正態分布![]() ,且不影響產量.請你幫該公司作出決策,是否要購買該設備?說明理由.
,且不影響產量.請你幫該公司作出決策,是否要購買該設備?說明理由.
(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com