精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

如圖，拋物線經過點、、，已知點，，且，點為拋物線上一點（異于）．

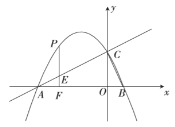
（1）求拋物線和直線的表達式．

（2）若點是直線上方拋物線上的點，過點作，與交于點，垂足為．當時，求點的坐標．

（3）若點為軸上一動點，是否存在點，使得由，，，四點組成的四邊形為平行四邊形？若存在，直接寫出點的坐標；若不存在，請說明理由．

在數學活動課上，老師出示了這樣一個問題：如圖1，在中，，，，點為邊上的任意一點．將沿過點的直線折疊，使點落在斜邊上的點處．問是否存在是直角三角形？若不存在，請說明理由；若存在，求出此時的長度．

探究展示：勤奮小組很快找到了點、的位置．

如圖2，作的角平分線交于點，此時沿所在的直線折疊，點恰好在上，且，所以是直角三角形．

問題解決:

（1）按勤奮小組的這種折疊方式，的長度為 ．

（2/span>）創新小組看完勤奮小組的折疊方法后，發現還有另一種折疊方法，請在圖3中畫出來．

（3）在（2）的條件下，求出的長．

“圓材埋壁”是我國古代數學著作《九章算術》中的一個問題：今有圓材，埋在壁中，不知大小，以鋸鋸之，深一寸，鋸道長一尺，問徑幾何？用現在的數學語言表達是：如圖，為的直徑，弦，垂足為，寸，尺，其中1尺寸，求出直徑的長．

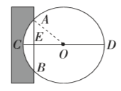
解題過程如下：

連接，設寸，則寸．

∵尺，∴寸．

在中，，即，解得，

∴寸．

任務：

（1）上述解題過程運用了 定理和 定理．

（2）若原題改為已知寸，尺，請根據上述解題思路，求直徑的長．

（3）若繼續往下鋸，當鋸到時，弦所對圓周角的度數為 ．

【題目】如圖，反比例函數y＝（k≠0，x＞0）的圖象與矩形OABC的邊AB、BC分別交于點E、F，E（，6），且E為BC的中點，D為x軸負半軸上的點．

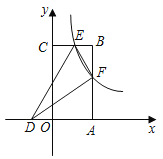
（1）求反比倒函數的表達式和點F的坐標；

（2）若D（﹣，0），連接DE、DF、EF，則△DEF的面積是　 ．

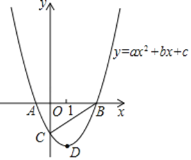
（1）求拋物線的解析式．

（2）點E為線段BC上一動點，過點E作x軸的垂線，與拋物線交于點F，求四邊形ACFB面積的最大值，以及此時點E的坐標．

（3）拋物線的對稱軸上是否存在一點P，使△PCD為等腰三角形？若存在，寫出點P點的坐標；若不存在，說明理由．

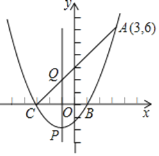
（1）求此二次函數的解析式；

（2）寫出不等式ax2+bx+c≥0的解集；

（3）設此拋物線的頂點為P，對稱軸與線段AC相交于點Q，求點P和點Q的坐標；

（4）在x軸上有一動點M，當MQ+MA取得最小值時，求M點的坐標．

（1）當銷售價為每件80元時，一周能銷售多少件？答：_____________件．

（2）寫出y與x的函數關系式，并寫出x的取值范圍.

（3）設一周的銷售利潤為w，寫出w與x的函數關系式.

（4）在超市對該種商品投入不超過18000元的情況下，使得一周銷售利潤達到8000元，銷售單價應定為多少？

【題目】如圖，正方形中，經順時針旋轉后與重合．

旋轉中心是點________，旋轉了________度；

如果，，求：四邊形的面積．

（1）畫出△ABC關于原點對稱的△A1B1C1；

（2）畫出△ABC向上平移5個單位后的△A2B2C2，并求出平移過程中△ABC掃過的面積．

【題目】如圖，點A是拋物線對稱軸上的一點，連接OA，以A為旋轉中心將AO逆時針旋轉90°得到AO′，當O′恰好落在拋物線上時，點A的坐標為______________．