
科目: 來源: 題型:
【題目】某學習小組做“用頻率估計概率”的實驗時,統計了某一結果出現的頻率,繪制了如下折線統計圖,則符合這一結果的實驗最有可能的是( )

A. 袋中裝有大小和質地都相同的3個紅球和2個黃球,從中隨機取一個,取到紅球
B. 擲一枚質地均勻的正六面體骰子,向上的面的點數是偶數
C. 先后兩次擲一枚質地均勻的硬幣,兩次都出現反面
D. 先后兩次擲一枚質地均勻的正六面體骰子,兩次向上的面的點數之和是7或超過9
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a>0)的頂點為M,直線y=m與拋物線交于點A,B,若△AMB為等腰直角三角形,我們把拋物線上A,B兩點之間的部分與線段AB 圍成的圖形稱為該拋物線對應的準蝶形,線段AB稱為碟寬,頂點M 稱為碟頂.

(1)由定義知,取AB中點N,連結MN,MN與AB的關系是_____.
(2)拋物線y=![]() 對應的準蝶形必經過B(m,m),則m=_____,對應的碟寬AB是_____.
對應的準蝶形必經過B(m,m),則m=_____,對應的碟寬AB是_____.
(3)拋物線y=ax2﹣4a﹣![]() (a>0)對應的碟寬在x 軸上,且AB=6.
(a>0)對應的碟寬在x 軸上,且AB=6.
①求拋物線的解析式;
②在此拋物線的對稱軸上是否有這樣的點P(xp,yp),使得∠APB為銳角,若有,請求出yp的取值范圍.若沒有,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,A(0,2),B(6,2),C(0,c)(c>0),以A為圓心AB長為半徑的![]() 交y軸正半軸于點D,
交y軸正半軸于點D,![]() 與BC有交點時,交點為E,P為
與BC有交點時,交點為E,P為![]() 上一點.
上一點.
(1)若c=6![]() +2,
+2,
①BC=_____,![]() 的長為_____;
的長為_____;
②當CP=6![]() 時,判斷CP與⊙A的位置關系,并加以證明;
時,判斷CP與⊙A的位置關系,并加以證明;
(2)若c=10,求點P與BC距離的最大值;
(3)分別直接寫出當c=1,c=6,c=9,c=11時,點P與BC的最大距離(結果無需化簡)

查看答案和解析>>
科目: 來源: 題型:
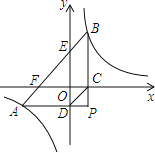
【題目】如圖,![]() 的直角頂點P在第四象限,頂點A、B分別落在反比例函數
的直角頂點P在第四象限,頂點A、B分別落在反比例函數![]() 圖象的兩支上,且
圖象的兩支上,且![]() 軸于點C,
軸于點C,![]() 軸于點D,AB分別與x軸,y軸相交于點F和
軸于點D,AB分別與x軸,y軸相交于點F和![]() 已知點B的坐標為
已知點B的坐標為![]() .
.
![]() 填空:
填空:![]() ______;
______;
![]() 證明:
證明:![]() ;
;
![]() 當四邊形ABCD的面積和
當四邊形ABCD的面積和![]() 的面積相等時,求點P的坐標.
的面積相等時,求點P的坐標.
查看答案和解析>>
科目: 來源: 題型:
【題目】八年級(1)班學生在完成課題學習“體質健康測試中的數據分析”后,利用課外活動時間積極參加體育鍛煉,每位同學從籃球、跳繩、立定跳遠、長跑、鉛球中選一項進行訓練,訓練后都進行了測試.現將項目選擇情況及訓練后籃球定時定點投籃測試成績整理后作出如下統計圖.
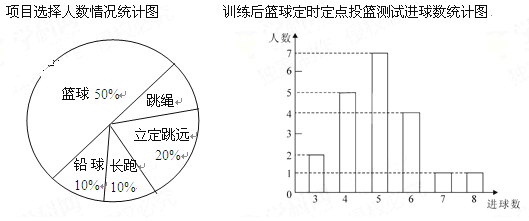
請你根據上面提供的信息回答下列問題:
(1)扇形圖中跳繩部分的扇形圓心角為 度,該班共有學生 人, 訓練后籃球定時定點投籃平均每個人的進球數是 .
(2)老師決定從選擇鉛球訓練的3名男生和1名女生中任選兩名學生先進行測試,請用列表或畫樹形圖的方法求恰好選中兩名男生的概率.
查看答案和解析>>
科目: 來源: 題型:
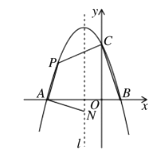
【題目】如圖,拋物線與![]() 軸交于點
軸交于點![]() 和點
和點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,其對稱軸
,其對稱軸![]() 為
為![]() ,
,![]() 為拋物線上第二象限的一個動點.
為拋物線上第二象限的一個動點.
(1)求拋物線的解析式并寫出其頂點坐標;
(2)當點![]() 在運動過程中,求四邊形
在運動過程中,求四邊形![]() 面積最大時的值及此時點
面積最大時的值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目: 來源: 題型:
【題目】(1)【問題發現】
如圖1,在Rt△ABC中,AB=AC=2,∠BAC=90°,點D為BC的中點,以CD為一邊作正方形CDEF,點E恰好與點A重合,則線段BE與AF的數量關系為
(2)【拓展研究】
在(1)的條件下,如果正方形CDEF繞點C旋轉,連接BE,CE,AF,線段BE與AF的數量關系有無變化?請僅就圖2的情形給出證明;
(3)【問題發現】
當正方形CDEF旋轉到B,E,F三點共線時候,直接寫出線段AF的長.

查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,有長為 24m 的籬笆,現一面利用墻(墻的最大可用長度 a 為 10m)圍成中間隔有一道籬笆的長方形花圃,設花圃的寬 AB 為 xm,面積為 Sm2.
(1) 求 S 與 x 的函數關系式及 x 值的取值范圍;
(2) 要圍成面積為 45m2 的花圃,AB 的長是多少米?
(3) 當 AB 的長是多少米時,圍成的花圃的面積最大?

查看答案和解析>>
科目: 來源: 題型:
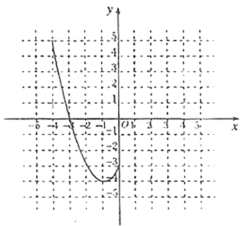
【題目】某班“數學興趣小組”對函數![]() 的圖像和性質進行了探究,探究過程如下,請補充完整.
的圖像和性質進行了探究,探究過程如下,請補充完整.
(1)自變量![]() 的取值范圍是全體實數,
的取值范圍是全體實數,![]() 與
與![]() 的幾組對應值列表如下:
的幾組對應值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ________________.
________________.
(2)根據上表數據,在如圖所示的平面直角坐標系中描點,并畫出了函數圖像的一部分,請畫出該圖像的另一部分;
(3)觀察函數圖像,寫出兩條函數的性質;
(4)進一步探究函數圖像發現:
①方程![]() 有______個實數根;
有______個實數根;
②函數圖像與直線![]() 有_______個交點,所以對應方程
有_______個交點,所以對應方程![]() 有_____個實數根;
有_____個實數根;
③關于![]() 的方程
的方程![]() 有
有![]() 個實數根,
個實數根,![]() 的取值范圍是___________.
的取值范圍是___________.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,建筑物AB的高為6cm,在其正東方向有個通信塔CD,在它們之間的地面點M(B,M,D三點在一條直線上)處測得建筑物頂端A、塔項C的仰角分別為37°和60°,在A處測得塔頂C的仰角為30°,則通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() =1.73,精確到0.1m)
=1.73,精確到0.1m)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com