【題目】如果把一個自然數各數位上數字從最高位到個位依次排出一串數字，與從個位到最高位依次排出的一串數字完全相同，那么我們把這樣的自然數叫做 “和諧數”．例如：自然數64746從最高位到個位排出的一串數字是：6、4、7、4、6，從個位到最高排出的一串數字也是：6、4、7、4、6，所64746是“和諧數”．再如：33，181，212，4664，…，都是“和諧數”．
（1）請你直接寫出3個四位“和諧數”，猜想任意一個四位“和諧數”能否被11整除，并說明理由；[來。
（2） 已知一個能被11整除的三位“和諧數”，設個位上的數字為x（
，x為自然數），十位上的數字為y，求y與x的函數關系式．
【答案】見解析，能被11整除；y=2x（1≤x≤4）
【解析】試題分析：根據“和諧數”的定義寫出數字，然后設“和諧數”的形式為abcd，則根據題意得出a=d，b=c，然后將這個四位數除以11，將其化成代數式的形式，用a和b來表示c和d，然后得出答案，進行說明能被11整除；首先設三位“和諧數”為zyx，根據定義得出x=z，然后根據同上的方法進行計算．
試題解析：⑴、四位“和諧數”：1221，1331，1111，6666…（答案不唯一）
任意一個四位“和諧數”都能被11整數，理由如下：
設任意四位“和諧數”形式為： 
，則滿足：
最高位到個位排列： 
個位到最高位排列： 
由題意，可得兩組數據相同，則： 
則
∴ 四位“和諧數”
能被11整數 又∵
為任意自然數，
∴任意四位“和諧數”都可以被11整除
⑵、設能被11整除的三位“和諧數”為： 
，則滿足：個位到最高位排列： 
最高位到個位排列： 
由題意，兩組數據相同，則： 
故
為正整數 ∴
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，我們定義直線y=ax﹣a為拋物線
（a、b、c為常數，a≠0）的“夢想直線”；有一個頂點在拋物線上，另有一個頂點在y軸上的三角形為其“夢想三角形”．
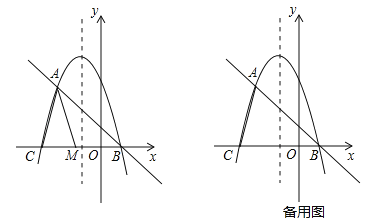
已知拋物線
與其“夢想直線”交于A、B兩點（點A在點B的左側），與x軸負半軸交于點C．
（1）填空：該拋物線的“夢想直線”的解析式為 ，點A的坐標為 ，點B的坐標為 ；
（2）如圖，點M為線段CB上一動點，將△ACM以AM所在直線為對稱軸翻折，點C的對稱點為N，若△AMN為該拋物線的“夢想三角形”，求點N的坐標；
（3）當點E在拋物線的對稱軸上運動時，在該拋物線的“夢想直線”上，是否存在點F，使得以點A、C、E、F為頂點的四邊形為平行四邊形？若存在，請直接寫出點E、F的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在△ABC中，分別延長△ABC的邊AB，AC到D，E，∠CBD與∠BCE的平分線相交于點P，愛動腦筋的小明在寫作業時發現如下規律：
①若∠A＝50°，則∠P＝65°＝90°－
；
②若∠A＝90°，則∠P＝45°＝90°－
；
③若∠A＝100°，則∠P＝40°＝90°－
.
(1)根據上述規律，若∠A＝150°，則∠P＝________；
(2)請你用數學表達式寫出∠P與∠A的關系；
(3)請說明(2)中結論的正確性．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列命題中，正確的有（ ）
①Rt△ABC中，已知兩邊長分別為3和4，則第三邊長為5；
②有一個內角等于其他兩個內角和的三角形是直角三角形；
③三角形的三邊分別為a，b，C，若a2+c2=b2，那么∠C=90°；
④若△ABC中，∠A：∠B：∠C=1：5：6，則△ABC是直角三角形．
A．1個 B．2個 C．3個 D．4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知直線AB∥CD．
（1）如圖1，直接寫出∠ABE，∠CDE和∠BED之間的數量關系是 ．
（2）如圖2，BF，DF分別平分∠ABE，∠CDE，那么∠BFD和∠BED有怎樣的數量關系？請說明理由．
（3）如圖3，點E在直線BD的右側，BF，DF仍平分∠ABE，∠CDE，請直接寫出∠BFD和∠BED的數量關系 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
