
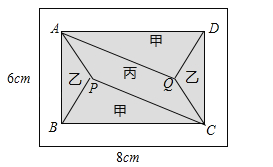
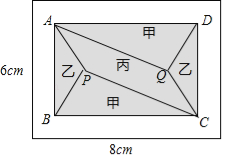
【題目】(2017浙江省溫州市)小黃準備給長8m,寬6m的長方形客廳鋪設瓷磚,現將其劃分成一個長方形ABCD區域Ⅰ(陰影部分)和一個環形區域Ⅱ(空白部分),其中區域Ⅰ用甲、乙、丙三種瓷磚鋪設,且滿足PQ∥AD,如圖所示.
(1)若區域Ⅰ的三種瓷磚均價為300元/m2,面積為S(m2),區域Ⅱ的瓷磚均價為200元/m2,且兩區域的瓷磚總價為不超過12000元,求S的最大值;
(2)若區域Ⅰ滿足BC=2:3,區域Ⅱ四周寬度相等.
①求AB,BC的長;
②若甲、丙兩瓷磚單價之和為300元/m2,乙、丙瓷磚單價之比為5:3,且區域Ⅰ的三種瓷磚總價為4800元,求丙瓷磚單價的取值范圍.
【答案】(1)24;(2)①AB=4,CB=6;②丙瓷磚單價3x的范圍為150<3x<300元/m2.
【解析】試題(1)根據題意可得300S+(48﹣S)200≤12000,解不等式即可;
(2)①設區域Ⅱ四周寬度為a,則由題意(6﹣2a):(8﹣2a)=2:3,解得a=1,由此即可解決問題;
②設乙、丙瓷磚單價分別為5x元/m2和3x元/m2,則甲的單價為(300﹣3x)元/m2,由PQ∥AD,可得甲的面積=矩形ABCD的面積的一半=12,設乙的面積為s,則丙的面積為(12﹣s),由題意12(300﹣3x)+5xs+3x(12﹣s)=4800,解得s=![]() ,由0<s<12,可得0<
,由0<s<12,可得0<![]() <12,解不等式即可
<12,解不等式即可
試題解析:(1)由題意300S+(48﹣S)200≤12000,
解得S≤24.
∴S的最大值為24.
(2)①設區域Ⅱ四周寬度為a,則由題意(6﹣2a):(8﹣2a)=2:3,解得a=1,
∴AB=6﹣2a=4,CB=8﹣2a=6.
②設乙、丙瓷磚單價分別為5x元/m2和3x元/m2,則甲的單價為(300﹣3x)元/m2,
∵PQ∥AD,
∴甲的面積=矩形ABCD的面積的一半=12,設乙的面積為s,則丙的面積為(12﹣s),
由題意12(300﹣3x)+5xs+3x(12﹣s)=4800,
解得s=![]() ,
,
∵0<s<12,
∴0<![]() <12,
<12,
∴0<x<50,
∴丙瓷磚單價3x的范圍為0<3x<150元/m2.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
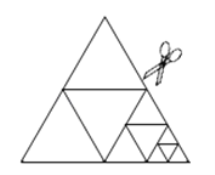
【題目】如圖,將一張正三角形紙片剪成四個小正三角形,得到![]() 個小正三角形,稱為第一次操作; 然后,將其中的一個正三角形再剪成四個小正三角形,共得到
個小正三角形,稱為第一次操作; 然后,將其中的一個正三角形再剪成四個小正三角形,共得到![]() 個小正三角形,稱為第二次操作;再將其中的一個正三角形再剪成四個小正三角形,共得到
個小正三角形,稱為第二次操作;再將其中的一個正三角形再剪成四個小正三角形,共得到![]() 個小正三角形,稱為第三次操作;…,根據以上操作,若要得到
個小正三角形,稱為第三次操作;…,根據以上操作,若要得到![]() 個小正三角形,則需要操作的次數是__________次.
個小正三角形,則需要操作的次數是__________次.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() ,一次函數
,一次函數![]() 的圖像過點
的圖像過點![]() ,且與
,且與![]() 軸及
軸及![]() 的圖像分別交于點
的圖像分別交于點![]() 、
、![]() ,
,![]() 點坐標為
點坐標為![]() .
.
(1)求n的值及一次函數![]() 的解析式.
的解析式.
(2)求四邊形![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系xOy中的點P(a,b),若點P′的坐標為(a+kb,ka+b)(其中k為常數,且k≠0),
則稱點P′為點P的“k屬派生點”.例如:P(1,4)的“2屬派生點”為P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)點P(﹣2,3)的“3屬派生點”P′的坐標為 ;
(Ⅱ)若點P的“5屬派生點”P′的坐標為(3,﹣9),求點P的坐標;
(Ⅲ)若點P在x軸的正半軸上,點P的“k屬派生點”為P′點,且線段PP′的長度為線段OP長度的2倍,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠CAB=∠DBA,再添加一個條件,不一定能判定△ABC≌△BAD的是( )
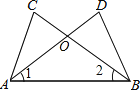
A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個自然數的立方,可以分裂成若干個連續奇數的和。例如:![]() 和
和![]() 分別可以按如圖所示的方式“分裂”成2個、3個和4個連續奇數的和,即
分別可以按如圖所示的方式“分裂”成2個、3個和4個連續奇數的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此規律來進行“分裂”,則
也按照此規律來進行“分裂”,則![]() “分裂”出的奇數中,最大的奇數是______.
“分裂”出的奇數中,最大的奇數是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點O是等邊三角形ABC內一點,∠AOB=110°,∠BOC=α, 以OC為邊作等邊三角形OCD,連接AD.

(1)當α=150°時,試判斷△AOD的形狀,并說明理由;
(2)探究:當a為多少度時,△AOD是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
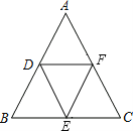
【題目】如圖,在△ABC中,∠B=∠C=∠DEF,點D、E、F分別在AB、AC上,且BD=CE.求證:DE=EF.
證明:(請將下面的證明過程補充完整)
∵∠B+∠BDE+∠BED=180°(______)
∠DEF+∠FEC+∠BED=180°(______)
∠B=∠DEF(已知)
∴∠BDE=∠FEC(______)
在△BDE和△CEF中
∠B=∠C(已知)
BD=CE(______)
∠BDE=∠FEC(______)
∴△BDE≌△CEF(______)(用字母表示)
∴DE=EF(______)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分別填入它所屬于的集合的括號內.
9,![]() ,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
正分數集合{_________}
負分數集合{_________}
負整數集合{__________}
非負整數集合{________}.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com