
【題目】幾何計算:
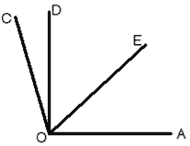
(1)如圖:已知AB=9cm,BD=3cm,C為AB的中點,求線段DC的長.
![]()
(2)如圖,OE為∠AOD的平分線,∠COD=![]() ∠EOC,∠COD=15°,求:
∠EOC,∠COD=15°,求:
①∠EOC的大小;
②∠AOD的大小.
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
在學習“分式方程及其解法”過程中,老師提出一個問題:若關于x的分式方程![]() 的解為正數,求a的取值范圍?
的解為正數,求a的取值范圍?
經過獨立思考與分析后,小明和小聰開始交流解題思路如下:
小明說:解這個關于x的分式方程,得到方程的解為![]() .由題意可得
.由題意可得![]() ,所以
,所以![]() ,問題解決.
,問題解決.
小聰說:你考慮的不全面.還必須保證![]() 才行.
才行.
請回答:_______________的說法是正確的,并說明正確的理由是:__________________.
完成下列問題:
(1)已知關于x的方程![]() 的解為非負數,求m的取值范圍;
的解為非負數,求m的取值范圍;
(2)若關于x的分式方程![]() 無解.直接寫出n的取值范圍.
無解.直接寫出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
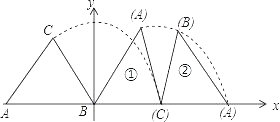
【題目】等腰三角形ABC在平面直角坐標系中的位置如圖所示,已知點A(﹣6,0),點B在原點,CA=CB=5,把等腰三角形ABC沿x軸正半軸作無滑動順時針翻轉,第一次翻轉到位置①,第二次翻轉到位置②…依此規律,第18次翻轉后點C的縱坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列解題過程的空白處填上適當的內容(推理的理由或數學表達式)
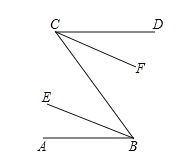
如圖,已知AB∥CD,BE、CF分別平分∠ABC和∠DCB,求證:BE∥CF.
證明:∵AB∥CD,(已知)
∴∠_______=∠_______.___________________________
∵__________________________________________,(已知)
∴∠EBC=_______,(角平分線定義)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性質)
∴BE//CF.(_____________________________________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若直線l1經過點(0,4),l2經過(3,2),且l1與l2關于x軸對稱,則l1與l2的交點坐標為
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形A1B1C1O,正方形A2B2C2C1,正方形A3B3C3C2,…按如圖所示的方式放置在平面直角坐標系中.點A1,A2,A3…和點C1,C2,C3,…分別在直線y=x+1和x軸上,則點Bn的坐標是__________.(n為正整數)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】益馬高速通車后,將桃江馬跡塘的農產品運往益陽的運輸成本大大降低。馬跡塘一農戶需要將A,B兩種農產品定期運往益陽某加工廠,每次運輸A,B產品的件數不變,原來每運一次的運費是1200元,現在每運一次的運費比原來減少了300元,A,B兩種產品原來的運費和現在的運費(單位:元∕件)如下表所示:
品種 | A | B |
原來的運費 | 45 | 25 |
現在的運費 | 30 | 20 |
(1)求每次運輸的農產品中A,B產品各有多少件?
(2)由于該農戶誠實守信,產品質量好,加工廠決定提高該農戶的供貨量,每次運送的總件數增加8件,但總件數中B產品的件數不得超過A產品件數的2倍,問產品件數增加后,每次運費最少需要多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年《政府工作報告》中提出了十大新詞匯,為了解同學們對新詞匯的關注度,某數學興趣小組選取其中的A:“互聯網+政務服務”,B:“工匠精神”,C:“光網城市”,D:“大眾旅游時代”四個熱詞在全校學生中進行了抽樣調查,要求被調查的每位同學只能從中選擇一個我最關注的熱詞.根據調查結果,該小組繪制了如下的兩幅不完整的統計圖. 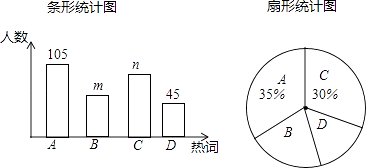
請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了多少名同學?
(2)條形統計圖中,m= , n=;
(3)扇形統計圖中,熱詞B所在扇形的圓心角是多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,AC的垂直平分線分別與AC,BC及AB的延長線相交于點D,E,F,且BF=BC.⊙O是△BEF的外接圓,∠EBF的平分線交EF于點G,交⊙O于點H,連接BD,FH. 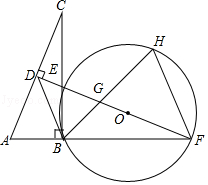
(1)求證:△ABC≌△EBF;
(2)試判斷BD與⊙O的位置關系,并說明理由;
(3)若AB=1,求HGHB的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com