
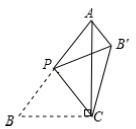
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是
是![]() 邊上的動(dòng)點(diǎn)(不與點(diǎn)
邊上的動(dòng)點(diǎn)(不與點(diǎn)![]() 重合),將
重合),將![]() 沿
沿![]() 所在的直線翻折,得到
所在的直線翻折,得到![]() ,連接
,連接![]() ,則下列判斷:
,則下列判斷:
①當(dāng)![]() 時(shí),
時(shí),![]()
②當(dāng)![]() 時(shí),
時(shí),![]()
③當(dāng)![]() 時(shí),
時(shí),![]() ;
;
④![]() 長度的最小值是1.
長度的最小值是1.
其中正確的判斷是______(填入正確結(jié)論的序號(hào))
【答案】①②④
【解析】
①由直角三角形斜邊上的中線等于斜邊的一半以及折疊的性質(zhì),易得![]() ,即可得
,即可得![]() ;
;
②由![]() ,可得點(diǎn)
,可得點(diǎn)![]() 在以
在以![]() 為圓心,
為圓心,![]() 長為半徑的圓上,然后在由圓周角定理,求得答案;
長為半徑的圓上,然后在由圓周角定理,求得答案;
③當(dāng)![]() 時(shí),易得
時(shí),易得![]() ,再根據(jù)相似三角形對(duì)應(yīng)邊成比例,求得AP的長;
,再根據(jù)相似三角形對(duì)應(yīng)邊成比例,求得AP的長;
④易得![]() ,
,![]() 長度的最小值是1.
長度的最小值是1.
解:①∵在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
由折疊的性質(zhì)可得:![]()
∴![]() ,
,
![]()
∴![]()
∴![]() ;故①正確;
;故①正確;
②∵![]() ,
,
∴![]() ,
,
∴點(diǎn)![]() 在以
在以![]() 為圓心,
為圓心,![]() 長為半徑的圓上,
長為半徑的圓上,
∵由折疊的性質(zhì)可得:![]() ,
,
∴![]() ,
,
∴![]() 故②正確
故②正確
③當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
∵在![]() 中,由勾股定理可知
中,由勾股定理可知![]()
∴![]() 故③錯(cuò)誤;
故③錯(cuò)誤;
④由軸對(duì)稱的性質(zhì)可知:![]() ,
,
∵![]() 長度固定不變,
長度固定不變,
∵![]()
![]()
∴![]() 的長度有最小值.
的長度有最小值.
![]() 有最小值
有最小值![]() .故④正確.
.故④正確.
故答案為:①②④


 口算題卡加應(yīng)用題集訓(xùn)系列答案
口算題卡加應(yīng)用題集訓(xùn)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,AB是⊙O直徑,OD⊥弦BC于點(diǎn)F,且交⊙O于點(diǎn)E,若∠AEC=∠ODB.
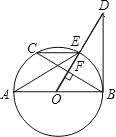
(1)求證:BD是⊙O的切線;
(2)當(dāng)AB=10,BC=8時(shí),求BD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場家電專柜購進(jìn)一批甲,乙兩種電器,甲種電器共用了10 350元,乙種電器共用了9 600元,甲種電器的件數(shù)是乙種電器的1.5倍,甲種電器每件的進(jìn)價(jià)比乙種電器每件的進(jìn)價(jià)少90元.
(1)甲、乙兩種電器各購進(jìn)多少件?
(2)商場購進(jìn)兩種電器后,按進(jìn)價(jià)提高40%后標(biāo)價(jià)銷售,很快全部售完,求售完這批電器商場共獲利多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】每到春夏交替時(shí)節(jié),雌性楊樹會(huì)以滿天飛絮的方式來傳播下一代,漫天飛舞的楊絮易引發(fā)皮膚病、呼吸道疾病等,給人們?cè)斐衫_,為了解市民對(duì)治理?xiàng)钚醴椒ǖ馁澩闆r,某課題小組隨機(jī)調(diào)查了部分市民(問卷調(diào)查表如表所示),并根據(jù)調(diào)查結(jié)果繪制了如下尚不完整的統(tǒng)計(jì)圖.
治理?xiàng)钚跻灰荒x哪一項(xiàng)?(單選)
A.減少楊樹新增面積,控制楊樹每年的栽種量
B.調(diào)整樹種結(jié)構(gòu),逐漸更換現(xiàn)有楊樹
C.選育無絮楊品種,并推廣種植
D.對(duì)雌性楊樹注射生物干擾素,避免產(chǎn)生飛絮
E.其他
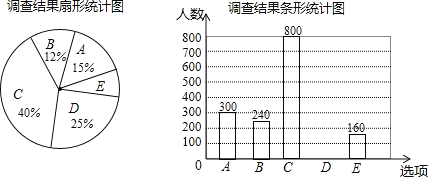
根據(jù)以上統(tǒng)計(jì)圖,解答下列問題:
(1)本次接受調(diào)查的市民共有 人;
(2)扇形統(tǒng)計(jì)圖中,扇形E的圓心角度數(shù)是 ;
(3)請(qǐng)補(bǔ)全條形統(tǒng)計(jì)圖;
(4)若該市約有90萬人,請(qǐng)估計(jì)贊同“選育無絮楊品種,并推廣種植”的人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,點(diǎn)
中,點(diǎn)![]() 是線段
是線段![]() 上的動(dòng)點(diǎn),將線段
上的動(dòng)點(diǎn),將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 得到線段
得到線段![]() ,連接
,連接![]() .若已知
.若已知![]() ,設(shè)
,設(shè)![]() 兩點(diǎn)間的距離為
兩點(diǎn)間的距離為![]() 兩點(diǎn)間的距離為
兩點(diǎn)間的距離為![]() 兩點(diǎn)間的距離為
兩點(diǎn)間的距離為![]() .(若同學(xué)們打印的BC的長度如不是
.(若同學(xué)們打印的BC的長度如不是![]() ,請(qǐng)同學(xué)們重新畫圖、測量)
,請(qǐng)同學(xué)們重新畫圖、測量)
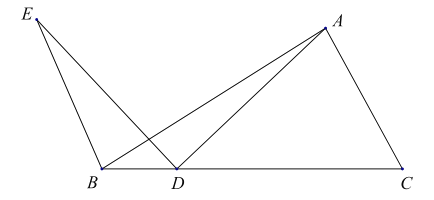
小明根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),分別對(duì)![]() 自變量x的變化而變化的規(guī)律進(jìn)行了探究,下面是小明的探究過程,請(qǐng)補(bǔ)充完整:
自變量x的變化而變化的規(guī)律進(jìn)行了探究,下面是小明的探究過程,請(qǐng)補(bǔ)充完整:
(1)按照下表中自變量![]() 的值進(jìn)行取點(diǎn)、畫圖、測量,分別得到了
的值進(jìn)行取點(diǎn)、畫圖、測量,分別得到了![]() 與
與![]() 的幾組對(duì)應(yīng)值,如下表:
的幾組對(duì)應(yīng)值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
寫出![]() 的值.(保留1位小數(shù))
的值.(保留1位小數(shù))
(2)在同一平面直角坐標(biāo)系![]() 中,描出補(bǔ)全后的表中各組數(shù)值所對(duì)應(yīng)的點(diǎn)
中,描出補(bǔ)全后的表中各組數(shù)值所對(duì)應(yīng)的點(diǎn)![]() ,并畫出函數(shù)
,并畫出函數(shù)![]() 的圖象;
的圖象;
(3)結(jié)合函數(shù)圖像,解決問題:
①當(dāng)![]() 在線段
在線段![]() 上時(shí),
上時(shí),![]() 的長度約為________
的長度約為________![]() ;
;
②當(dāng)![]() 為等腰三角形時(shí),
為等腰三角形時(shí),![]() 的長度
的長度![]() 約為_______
約為_______![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于平面內(nèi)![]() 和
和![]() 外一點(diǎn)
外一點(diǎn)![]() ,若過點(diǎn)
,若過點(diǎn)![]() 的直線
的直線![]() 與
與![]() 有兩個(gè)不同的公共點(diǎn)
有兩個(gè)不同的公共點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為直線
為直線![]() 上的另一點(diǎn),且滿足
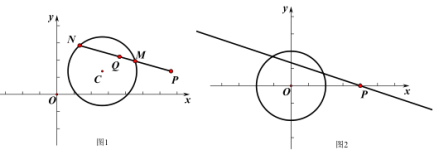
上的另一點(diǎn),且滿足![]() (如圖1所示),則稱點(diǎn)
(如圖1所示),則稱點(diǎn)![]() 是點(diǎn)
是點(diǎn)![]() 關(guān)于
關(guān)于![]() 的密切點(diǎn).
的密切點(diǎn).
已知在平面直角坐標(biāo)系![]() 中,
中, ![]() 的半徑為2,點(diǎn)
的半徑為2,點(diǎn)![]() .
.
(1)在點(diǎn)![]()
![]() 中,是點(diǎn)
中,是點(diǎn)![]() 關(guān)于
關(guān)于![]() 的密切點(diǎn)的為__________.
的密切點(diǎn)的為__________.
(2)設(shè)直線![]() 方程為
方程為![]() ,如圖2所示,
,如圖2所示,
①![]() 時(shí),求出點(diǎn)
時(shí),求出點(diǎn)![]() 關(guān)于
關(guān)于![]() 的密切點(diǎn)
的密切點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②![]() 的圓心為
的圓心為![]() ,半徑為2,若
,半徑為2,若![]() 上存在點(diǎn)
上存在點(diǎn)![]() 關(guān)于
關(guān)于![]() 的密切點(diǎn),直接寫出
的密切點(diǎn),直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
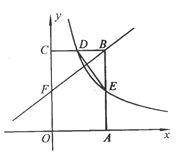
【題目】如圖,矩形OABC的頂點(diǎn)A、C分別在x軸和y軸上,點(diǎn)B的坐標(biāo)為(2,4),雙曲線![]() 的圖像經(jīng)過BC的中點(diǎn)D,且與AB交于點(diǎn)E,連接DE.
的圖像經(jīng)過BC的中點(diǎn)D,且與AB交于點(diǎn)E,連接DE.
(1)求k的值及點(diǎn)E的坐標(biāo);
(2)若點(diǎn)F是邊上一點(diǎn),且△FBC∽△DEB,求直線FB的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方形ABCD中,O是對(duì)角線AC與BD的交點(diǎn),M是BC邊上的動(dòng)點(diǎn)![]() 點(diǎn)M不與B,C重合
點(diǎn)M不與B,C重合![]() ,
,![]() ,CN與AB交于點(diǎn)N,連接OM,ON,
,CN與AB交于點(diǎn)N,連接OM,ON,![]() 下列五個(gè)結(jié)論:
下列五個(gè)結(jié)論:![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() ∽
∽![]() ;
;![]() ;
;![]() 若
若![]() ,則
,則![]() 的最小值是
的最小值是![]() ,其中正確結(jié)論的個(gè)數(shù)是
,其中正確結(jié)論的個(gè)數(shù)是![]()
![]()

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
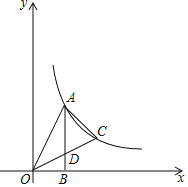
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)O為坐標(biāo)原點(diǎn),直角三角形AOB的直角頂點(diǎn)B在x軸正半軸上,點(diǎn)A在第一象限,OB=2,tan∠AOB=2.
(1)求圖象經(jīng)過點(diǎn)A的反比例函數(shù)的解析式;
(2)點(diǎn)C是(1)中反比例函數(shù)圖象上一點(diǎn),連接OC交AB于點(diǎn)D,連接AC,若D為OC中點(diǎn),求△ADC的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com