
【題目】已知m,n分別是關于x的一元二次方程ax2+bx+c=a與ax2+bx+c=b的一個根,且m=n+1.
(1)當m=2,a=﹣1時,求b與c的值;
(2)用只含字母a,n的代數式表示b;
(3)當a<0時,函數y=ax2+bx+c滿足b2﹣4ac=a,b+c≥2a,n≤﹣![]() ,求a的取值范圍.
,求a的取值范圍.
【答案】(1)b=1,c=1;(2)![]() ;(3)-
;(3)-![]() ≤a≤-
≤a≤-![]() .
.
【解析】
(1)由已知求出n,根據方程根的定義將m,n,a的值代入方程即可求解;
(2)根據方程根的定義將m,n的值代入方程消去c求解得到![]() ,再利用m+n=1,消去m,即可求出b只用字母a、n表示代數式,
,再利用m+n=1,消去m,即可求出b只用字母a、n表示代數式,
(3)將(2)結論![]() 代入方程
代入方程![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,繼而可得
,繼而可得![]() ,根據n的取值范圍即可確定a的取值范圍.
,根據n的取值范圍即可確定a的取值范圍.
(1)因為m,n分別是關于x的一元二次方程![]() 與
與![]() 的一個根,
的一個根,
所以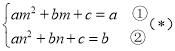 ,
,
由m=n+1,m=2得n = 1
把n=1,m=2,a = -1,代入(*)得,
![]() ,
,
解得![]() ;
;
(2)由(1)的方程組(*)中①-②,得
![]() ,
,
![]() ,由m=n+1,得m-n=1,
,由m=n+1,得m-n=1,
故a![]() ,
,
所以![]() ,
,
從而![]() ;
;
(3)把![]() 代入方程組(*)中②,得
代入方程組(*)中②,得
![]() ,
,
由![]() ≥2a得
≥2a得
![]() ≥2a,
≥2a,
當a<0時,n≥-1,
由n≤-![]() 得,-1≤n≤-
得,-1≤n≤-![]() ,
,
由![]() ,且
,且![]() ,得
,得
![]() ,
,
整理得,![]() ,因為a<0
,因為a<0
所以,![]() ,
,
即![]() ,
,
由于![]() 在-1≤n≤-
在-1≤n≤-![]() 時隨n的增大而增大,
時隨n的增大而增大,
所以當n= -1時,a= -![]() ,當n= -
,當n= -![]() 時,a= -
時,a= -![]()
即-![]() ≤a≤-
≤a≤-![]() .
.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在直角三角形ABC中,∠C=90°,AC=2,BC=2![]() ,點O是邊AB上的一個動點,以點O為圓心,OA為半徑作⊙O,與邊AC交于點M.
,點O是邊AB上的一個動點,以點O為圓心,OA為半徑作⊙O,與邊AC交于點M.
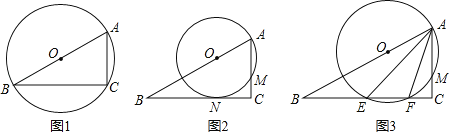
(1)如圖1,當⊙O經過點C時,⊙O的直徑是 ;
(2)如圖2,當⊙O與邊BC相切時,切點為點N,試求⊙O與△ABC重合部分的面積;
(3)如圖3,當⊙O與邊BC相交時,交點為E、F,設CM=x,就判斷AEAF是否為定值,若是,求出這個定值;若不是,請用含x的代數式表示.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】使用家用燃氣灶燒開同一壺水所需的燃氣量![]() (單位:
(單位:![]() )與旋鈕的旋轉角度
)與旋鈕的旋轉角度![]() (單位:度)(
(單位:度)(![]() )近似滿足函數關系y=ax2+bx+c(a≠0).如圖記錄了某種家用燃氣灶燒開同一壺水的旋鈕角度
)近似滿足函數關系y=ax2+bx+c(a≠0).如圖記錄了某種家用燃氣灶燒開同一壺水的旋鈕角度![]() 與燃氣量
與燃氣量![]() 的三組數據,根據上述函數模型和數據,可推斷出此燃氣灶燒開一壺水最節省燃氣的旋鈕角度約為( )
的三組數據,根據上述函數模型和數據,可推斷出此燃氣灶燒開一壺水最節省燃氣的旋鈕角度約為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() ,以點
,以點![]() 為圓心,線段
為圓心,線段![]() 的長為半徑畫弧,與直線
的長為半徑畫弧,與直線![]() 位于第一象限的部分相交于點
位于第一象限的部分相交于點![]() ,則點
,則點![]() 的坐標為_______.
的坐標為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
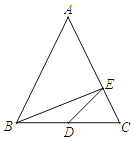
【題目】如圖,在△ABC中,AB=AC,BC=6,E為AC邊上的點且AE=2EC,點D在BC邊上且滿足BD=DE,設BD=y,S△ABC=x,則y與x的函數關系式為( )
A.y=![]() x2+
x2+![]() B.y=
B.y=![]() x2+
x2+![]()
C.y=![]() x2+2D.y=
x2+2D.y=![]() x2+2
x2+2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC于點D,點F為AB上一點,連接CF,過點B作BE⊥BC交CF的延長線于點E,交AD于點H,且∠1=∠2
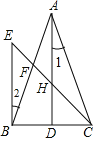
(1)求證:AB=AC;
(2)若∠1=22°,∠AFC=110°,求∠BCE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,反比例函數![]() (k是常數,且
(k是常數,且![]() )的圖象經過點
)的圖象經過點![]() .
.
(1)若b=4,求y關于x的函數表達式;
(2)點![]() 也在反比例函數y的圖象上:
也在反比例函數y的圖象上:
①當![]() 且
且![]() 時,求b的取值范圍;
時,求b的取值范圍;
②若B在第二象限,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
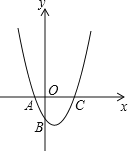
【題目】如圖示二次函數y=ax2+bx+c的對稱軸在y軸的右側,其圖象與x軸交于點A(﹣1,0)與點C(x2,0),且與y軸交于點B(0,﹣2),小強得到以下結論:①0<a<2;②﹣1<b<0;③c=﹣1;④當|a|=|b|時x2>![]() ﹣1;以上結論中正確結論的序號為 .
﹣1;以上結論中正確結論的序號為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com