
【題目】計算:
(1)(+10)+(﹣4)
(2)(﹣![]() )+(﹣
)+(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() ;
;
(3)5.6+(﹣0.9)+4.4+(﹣8.1)
(4)(﹣81)÷![]() ×
×![]() ÷(﹣16)
÷(﹣16)
(5)(﹣5)×49![]()
(6)(﹣125)×[2﹣(﹣2)]﹣300÷6.
【答案】(1)6;(2)-1;(3)1;(4)1;(5) -249![]() ;(6)-550;
;(6)-550;
【解析】
(1) 按有理數的加減運算法則進行運算即可;(2) (3)運用加法交換律進行簡便運算即可;(4)先化除為乘,然后按照有理數乘法的運算法則進行計算即可;(5) 逆用乘法分配律進行計算即可;(6)按照有理數的四則運算法則進行運算即可.
解:
(1)(+10)+(﹣4)=6
(2)(﹣![]() )+(﹣
)+(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() ;
;
=[(﹣![]() )+(﹣
)+(﹣![]() )]+[ (﹣
)]+[ (﹣![]() )+
)+![]() ]
]
=-1+0
=-1
(3)5.6+(﹣0.9)+4.4+(﹣8.1)
=5.6+4.4+[(﹣0.9)+(﹣8.1)]
=10-9
=1
(4)(﹣81)÷![]() ×
×![]() ÷(﹣16)
÷(﹣16)
=(﹣81)×![]() ×
×![]() ×(﹣
×(﹣![]() )
)
=-16×(﹣![]() )
)
=1
(5)(﹣5)×49![]()
=(﹣5)×(50-![]() )
)
=-250+![]()
=-249![]()
(6)(﹣125)×[2﹣(﹣2)]﹣300÷6.
=(﹣125)×4﹣300÷6
=-500-50
=-550


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】“直角”在初中數學學習中無處不在在數學活動課上,李老師要求同學們用所學知識,利用無刻度的直尺和圓規判斷“已知∠AOB“是不是直角.甲、乙兩名同學各自給出不同的作法,來判斷∠AOB是不是直角
甲:如圖1,在OA、OB上分別取點CD,以C為圓心,CD長為半徑畫弧,交OB的反向延長線于點E,若OE=OD,則∠AOB=90°;
乙:如圖2,在OA、OB上分別截取OM=4個單位長度,ON=3個單位長度,若MN=5個單位長度,則∠AOB=90°;
甲、乙兩位同學作法正確的是( )
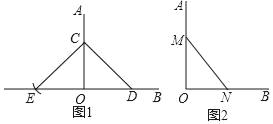
A. 甲正確,乙不正確B. 乙正確,甲不正確
C. 甲和乙都不正確D. 甲和乙都正確
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校計劃選購甲、乙兩種圖書作為“校園讀書節”的獎品.已知甲圖書的單價是乙圖書單價的![]() 倍;用
倍;用![]() 元單獨購買甲種圖書比單獨購買乙種圖書要少
元單獨購買甲種圖書比單獨購買乙種圖書要少![]() 本.
本.
(1)甲、乙兩種圖書的單價分別為多少元?
(2)若學校計劃購買這兩種圖書共![]() 本,且投入的經費不超過
本,且投入的經費不超過![]() 元,要使購買的甲種圖書數量不少于乙種圖書的數量,則共有幾種購買方案?
元,要使購買的甲種圖書數量不少于乙種圖書的數量,則共有幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰三角形ABC的底邊BC長為4,面積是16,腰AC的垂直平分線EF分別交AC,AB邊于E,F點,若點D為BC邊的中點,點M為線段EF上一動點,則![]() 周長的最小值為______.
周長的最小值為______.
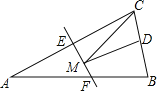
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB交x軸于點B(2,0),交y軸于點A(0,2),直線DM⊥x軸正半軸于點M,交線段AB于點C,DM=3,連接DA,∠DAC=90°.
(1)求直線AB的解析式.
(2)求D點坐標及過O、D、B三點的拋物線解析式.
(3)若點P是線段OB上的動點,過點P作x軸的垂線交AB于F,交(2)中拋物線于E,連CE,是否存在P使△BPF與△FCE相似?若存在,請求出P點坐標;若不存在說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=ax+b(a≠0)的圖象與反比例函數y=![]() (k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=
(k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=![]() ,點B的坐標為(m,-2).
,點B的坐標為(m,-2).
(1)求△AHO的周長;
(2)求該反比例函數和一次函數的解析式.

【答案】(1)△AHO的周長為12;(2) 反比例函數的解析式為y=![]() ,一次函數的解析式為y=-
,一次函數的解析式為y=-![]() x+1.
x+1.
【解析】試題分析: (1)根據正切函數,可得AH的長,根據勾股定理,可得AO的長,根據三角形的周長,可得答案;
(2)根據待定系數法,可得函數解析式.
試題解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周長=AO+AH+OH=3+4+5=12;
(2)將A點坐標代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函數的解析式為y=![]() ;
;
當y=-2時,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
將A、B點坐標代入y=ax+b,得
![]() ,
,
解得 ,
,
一次函數的解析式為y=-![]() x+1.
x+1.
考點:反比例函數與一次函數的交點問題.
【題型】解答題
【結束】
25
【題目】如圖,已知點A、C分別在∠GBE的邊BG、BE上,且AB=AC,AD∥BE,∠GBE的平分線與AD交于點D,連接CD.
求證:①AB=AD;
②CD平分∠ACE.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】花園內有一塊邊長為a的正方形土地,園藝師設計了四種不同的圖案,如下圖的A、B、C、D所示,其中的陰影部分用于種植花草.種植花草部分面積最大的圖案是( )(說明:A、B、C中圓弧的半徑均為![]() ,D中圓弧的半徑為a)
,D中圓弧的半徑為a)
A.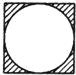 B.
B.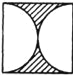 C.
C.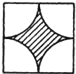 D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分別填入相應的集合里.
-4,![]() ,0,
,0,![]() ,-3.14,717,-(+5),+1.88,
,-3.14,717,-(+5),+1.88,![]()
(1)正數集合:{ … };
(2)負數集合:{ …};
(3)整數集合:{ …};
(4)分數集合:{ … }.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請根據圖中提供的信息,列一元一次方程解應用題,回答下列問題:
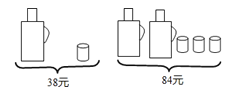
(1)求一個暖瓶與一個水杯分別是多少元?
(2)若買3個暖瓶與4個水杯一共需要多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com