
【題目】如圖,在平面直角坐標系中,一次函數y=ax+b(a≠0)的圖象與反比例函數y=![]() (k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=
(k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=![]() ,點B的坐標為(m,-2).
,點B的坐標為(m,-2).
(1)求△AHO的周長;
(2)求該反比例函數和一次函數的解析式.

【答案】(1)△AHO的周長為12;(2) 反比例函數的解析式為y=![]() ,一次函數的解析式為y=-
,一次函數的解析式為y=-![]() x+1.
x+1.
【解析】試題分析: (1)根據正切函數,可得AH的長,根據勾股定理,可得AO的長,根據三角形的周長,可得答案;
(2)根據待定系數法,可得函數解析式.
試題解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周長=AO+AH+OH=3+4+5=12;
(2)將A點坐標代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函數的解析式為y=![]() ;
;
當y=-2時,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
將A、B點坐標代入y=ax+b,得
![]() ,
,
解得 ,
,
一次函數的解析式為y=-![]() x+1.
x+1.
考點:反比例函數與一次函數的交點問題.
【題型】解答題
【結束】
25
【題目】如圖,已知點A、C分別在∠GBE的邊BG、BE上,且AB=AC,AD∥BE,∠GBE的平分線與AD交于點D,連接CD.
求證:①AB=AD;
②CD平分∠ACE.

科目:初中數學 來源: 題型:
【題目】觀察下面一列數,探究其中的規律:—1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)填空:第11,12,13三個數分別是 , , ;
(2)第2020個數是什么?
(3)如果這列數無限排列下去,與哪個數越來越近?
查看答案和解析>>
科目:初中數學 來源: 題型:
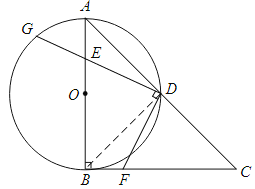
【題目】如圖,在RtΔABC中,∠ABC=90°,AB=CB,以AB為直徑的⊙O交AC于點D,點E是AB邊上一點(點E不與點A、B重合),DE的延長線交⊙O于點G,DF⊥DG,且交BC于點F.
(1)求證:AE=BF;
(2)連接EF,求證:∠FEB=∠GDA;
(3)連接GF,若AE=2,EB=4,求ΔGFD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件10元,出廠價為每件12元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=-10x+500.
(1)李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為W(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3000元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)(+10)+(﹣4)
(2)(﹣![]() )+(﹣
)+(﹣![]() )+(﹣
)+(﹣![]() )+
)+![]() ;
;
(3)5.6+(﹣0.9)+4.4+(﹣8.1)
(4)(﹣81)÷![]() ×
×![]() ÷(﹣16)
÷(﹣16)
(5)(﹣5)×49![]()
(6)(﹣125)×[2﹣(﹣2)]﹣300÷6.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“低碳環保,你我同行”.兩年來,揚州市區的公共自行車給市民出行帶來切實方便.電視臺記者在某區街頭隨機選取了市民進行調查,調查的問題是“您大概多久使用一次公共自行車?”,將本次調查結果歸為四種情況:A.每天都用;B.經常使用;C.偶爾使用;D.從未使用.將這次調查情況整理并繪制如下兩幅統計圖:

根據圖中的信息,解答下列問題:
(1)本次活動共有 位市民參與調查;
(2)補全條形統計圖;
(3)根據統計結果,若該區有46萬市民,請估算每天都用公共自行車的市民約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】右圖為手的示意圖,在各個手指之間標記字母A,B,C,D。請你按圖中箭頭所指的方向(即A→B→C→D→C→B→A→B→C→……的方式)從A開始數連續的正整數1,2,3,4,5,6,7,8,9,……

(1)當數到14時,對應的字母是_________;
(2)當字母C第201次出現時。恰好數到的數是_________;
(3)當字母C第2n+1次出現時(n為正整數),恰好數到的數是__________(用含有n的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠AOB和兩點C、D,求作一點P,使PC=PD,且點P到∠AOB的兩邊的距離相等.
(要求:用尺規作圖,保留作圖痕跡,寫出作法,不要求證明).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半徑為2的⊙C, 分別交AC、BC于點D、E,得到
.半徑為2的⊙C, 分別交AC、BC于點D、E,得到![]() .
.
(1)求證:AB為⊙C的切線;
(2)求圖中陰影部分的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com