
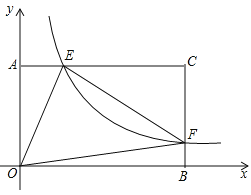
【題目】在矩形AOBC中,OB=6,OA=4,分別以OB,OA所在直線為x軸和y軸建立如圖所示的平面直角坐標(biāo)系,F是BC上的一個動點(diǎn)(不與B、C重合),過F點(diǎn)的反比例函數(shù)![]() (k>0)的圖象與AC邊交于點(diǎn)E,連接OE,OF,EF.
(k>0)的圖象與AC邊交于點(diǎn)E,連接OE,OF,EF.
(1)若tan∠BOF=![]() ,求F點(diǎn)的坐標(biāo);
,求F點(diǎn)的坐標(biāo);
(2)當(dāng)點(diǎn)F在BC上移動時,△OEF與△ECF的面積差記為S,求當(dāng)k為何值時,S有最大值,最大值是多少?
(3)是否存在這樣的點(diǎn)F,使得△OEF為直角三角形?若存在,求出此時點(diǎn)F坐標(biāo);若不存在,請說明理由。
【答案】(1). F(6,![]() );(2)當(dāng)k=12時,S最大為6;(3)F(6,
);(2)當(dāng)k=12時,S最大為6;(3)F(6,![]() ).
).
【解析】
(1)由tan∠BOF的值求出線段BF的長度,進(jìn)而得出點(diǎn)F的坐標(biāo);(2)設(shè)B(6,![]() ),分別表示出AE、CE、BF、CF的長度,進(jìn)而表示出△OEF與△ECF的面積,最后表示出S即可;(3)分類討論,根據(jù)相似三角形的判定與性質(zhì)列方程求解即可;
),分別表示出AE、CE、BF、CF的長度,進(jìn)而表示出△OEF與△ECF的面積,最后表示出S即可;(3)分類討論,根據(jù)相似三角形的判定與性質(zhì)列方程求解即可;
(1)tan∠BOF=![]() =
=![]() ,
,
∴BF=![]() ,
,
∴F(6,![]() );
);
(2)設(shè)B(6,![]() ),
),
令y=4,x=![]() ,
,
∴E(![]() ,4),
,4),
∴AE=![]() ,CE=6﹣
,CE=6﹣![]() ,BF=
,BF=![]() ,CF=4﹣
,CF=4﹣![]() ,
,
∴S△OEF=4×6﹣![]() ﹣
﹣![]() ﹣
﹣![]() ×(6﹣
×(6﹣![]() )×(4﹣
)×(4﹣![]() )=﹣
)=﹣![]() k2﹣2k+12,
k2﹣2k+12,
S△ECF=![]() ×(6﹣
×(6﹣![]() )×(4﹣
)×(4﹣![]() )=
)=![]() k2﹣k+12,
k2﹣k+12,
∴S△OEF﹣S△ECF=﹣![]() (k﹣12)2+6.
(k﹣12)2+6.
當(dāng)k=12時,S最大為6;
(3)①當(dāng)∠OEF=90°時,
∠AEO+∠CEF=90°,
∵∠CEF+∠CFE=90°,
∴∠AEO=∠CFE,
∵∠EAO=∠C=90°,
∴△EAO∽△FCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得k=24或![]() ,
,
∴F(4,6)(舍去)或(6,![]() ),
),
∴F(6,![]() );
);
②當(dāng)∠EFO=90°時,
同理可證△ECF∽△FBO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得k=54或24,
∴F(4,6)或(6,9),都不符合題意,
∴F(6,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
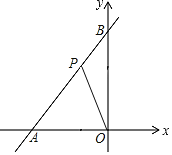
【題目】如圖,一次函數(shù)y=![]() x+4與x軸、y軸分別交于點(diǎn)A和點(diǎn)B,在線段AB上有一動點(diǎn)P(不與點(diǎn)A、B重合),連接OP,當(dāng)點(diǎn)P的坐標(biāo)為_____時線段OP最短.
x+4與x軸、y軸分別交于點(diǎn)A和點(diǎn)B,在線段AB上有一動點(diǎn)P(不與點(diǎn)A、B重合),連接OP,當(dāng)點(diǎn)P的坐標(biāo)為_____時線段OP最短.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線y=ax2+bx經(jīng)過點(diǎn)A(﹣1,![]() )及原點(diǎn),交x軸于另一點(diǎn)C(2,0),點(diǎn)D(0,m)是y軸正半軸上一動點(diǎn),直線AD交拋物線于另一點(diǎn)B.
)及原點(diǎn),交x軸于另一點(diǎn)C(2,0),點(diǎn)D(0,m)是y軸正半軸上一動點(diǎn),直線AD交拋物線于另一點(diǎn)B.
(1)求拋物線的解析式;
(2)如圖1,連接AO、BO,若△OAB的面積為5,求m的值;
(3)如圖2,作BE⊥x軸于E,連接AC、DE,當(dāng)D點(diǎn)運(yùn)動變化時,AC、DE的位置關(guān)系是否變化?請證明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方形ABCD中,點(diǎn)E,F(xiàn)分別是邊AD,BC的中點(diǎn),連接DF,過點(diǎn)E作EH⊥DF,垂足為H,EH的延長線交DC于點(diǎn)G.
(1)猜想DG與CF的數(shù)量關(guān)系,并證明你的結(jié)論;
(2)過點(diǎn)H作MN∥CD,分別交AD,BC于點(diǎn)M,N,若正方形ABCD的邊長為10,點(diǎn)P是MN上一點(diǎn),求△PDC周長的最小值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
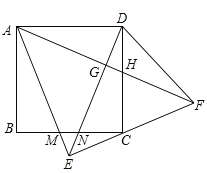
【題目】如圖,正方形ABCD中,以AD為底邊作等腰△ADE,將△ADE沿DE折疊,點(diǎn)A落到點(diǎn)F處,連接EF剛好經(jīng)過點(diǎn)C,再連接AF,分別交DE于點(diǎn)G,交CD于點(diǎn)H,下列結(jié)論:①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤![]() ,其中正確的有__________.
,其中正確的有__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】車間有20名工人,某天他們生產(chǎn)的零件個數(shù)統(tǒng)計如下表.
車間20名工人某一天生產(chǎn)的零件個數(shù)統(tǒng)計表
生產(chǎn)零件的個數(shù)(個) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人數(shù)(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求這一天20名工人生產(chǎn)零件的平均個數(shù);
(2)為了提高大多數(shù)工人的積極性,管理者準(zhǔn)備實(shí)行“每天定額生產(chǎn),超產(chǎn)有獎”的措施.如果你是管理者,從平均數(shù)、中位數(shù)、眾數(shù)的角度進(jìn)行分析,你將如何確定這個“定額”?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,將正方形![]() 置于平面直角坐標(biāo)系中,其中
置于平面直角坐標(biāo)系中,其中![]() 邊在
邊在![]() 軸上,其余各邊均與坐標(biāo)軸平行.直線
軸上,其余各邊均與坐標(biāo)軸平行.直線![]() 沿
沿![]() 軸的負(fù)方向以每秒1個單位的速度平移,在平移的過程中,該直線被正方形
軸的負(fù)方向以每秒1個單位的速度平移,在平移的過程中,該直線被正方形![]() 的邊所截得的線段長為
的邊所截得的線段長為![]() ,平移的時間為
,平移的時間為![]() (秒),
(秒),![]() 與
與![]() 的函數(shù)圖象如圖2所示,則圖1中的點(diǎn)
的函數(shù)圖象如圖2所示,則圖1中的點(diǎn)![]() 的坐標(biāo)為__________,圖2中
的坐標(biāo)為__________,圖2中![]() 的值為__________.
的值為__________.


![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在線段
在線段![]() 上運(yùn)動(
上運(yùn)動(![]() 不與
不與![]() 、
、![]() 重合),連接
重合),連接![]() ,作
,作![]() ,
,![]() 交線段
交線段![]() 于
于![]() .
.

(1)當(dāng)![]() 時,
時,![]() ______________
______________![]() ;點(diǎn)
;點(diǎn)![]() 從
從![]() 向
向![]() 運(yùn)動時,
運(yùn)動時,![]() 逐漸變____________(填“大”或“小”);
逐漸變____________(填“大”或“小”);
(2)當(dāng)![]() 時,求證:
時,求證:![]() ,請說明理由;
,請說明理由;
(3)在點(diǎn)![]() 的運(yùn)動過程中,
的運(yùn)動過程中,![]() 的形狀也在改變,判斷當(dāng)
的形狀也在改變,判斷當(dāng)![]() 等于多少度時,
等于多少度時,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△CAD與△CEB都是等邊三角形,BD、EA的延長線相交于點(diǎn)F.
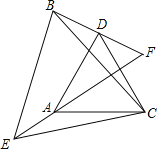
(1)求證:△ACE≌△DCB.
(2)求∠F的度數(shù).
(3)若AD⊥BD,請直接寫出線段EF與線段BD、DF之間的數(shù)量關(guān)系.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com