
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,
上,![]() 的平分線交
的平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .過點
.過點![]() 作
作![]() 的切線
的切線![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)求證:![]() ,
,![]() ;
;
(2)過點![]() 分別作直線
分別作直線![]() ,
,![]() 垂線,垂足為
垂線,垂足為![]() ,
,![]() .若
.若![]() ,
,![]() ,請你完成示意圖并求線段
,請你完成示意圖并求線段![]() 的長.
的長.
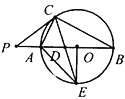
【答案】(1)證明見解析;(2)畫圖見解析,7
【解析】
(1)圖1中,連接![]() ,由AB是直徑可得
,由AB是直徑可得![]() ,由角平分線的定義可求∠ECA=45°,然后根據圓周角定理可求
,由角平分線的定義可求∠ECA=45°,然后根據圓周角定理可求![]() ;由OC=OE可證
;由OC=OE可證![]() ,然后利用余角的性質證明
,然后利用余角的性質證明![]() 可證
可證![]() ;
;
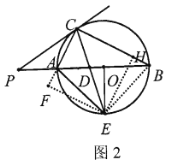
(2)如圖2中.作EH⊥BC于H,EF⊥CA于F.首先證明Rt△AEF≌Rt△BEH,推出AF=BH,設AF=BH=x,再證明四邊形CFEH是正方形,推出CF=CH,可得6+x=8-x,推出x=1即可解決問題;
(1)證明:①如圖1中,連接![]() ,
,
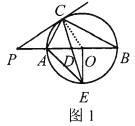
∵![]() 直徑,
直徑,
∴![]() ,
,
∴![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 是切線,
是切線,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)如圖2中,連接![]() ,過點
,過點![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .
.
又∵![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
由(1)得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,設
,設![]() ,
,
∵![]() ,
,
∴四邊形![]() 是矩形,
是矩形,
∵![]() ,
,
∴四邊形![]() 是正方形,
是正方形,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】“重慶自然博物館”坐落在美麗的縉云山腳下,該館現有藏品11萬余件,是全國中小學生研學實踐教育基地,西大附中某數學興趣小組,想測量博物館的高度,他們先在博物館正對面的大樓樓頂A處,測得博物館底部B處的俯角為50°,測得博物館頂端C的俯角為45°,再從樓底O經過平地到達F,再沿著斜坡向上到達E,最后經過平臺達到B,測得OF=20米,平臺EB的長為28.8米,已知,樓OA高為60.5米,斜坡EF的坡度i=1:2.4,A、O、F、E、B、C在同一平面內,則博物館的高約為( )米.(參考數據:tan50°≈1.2)
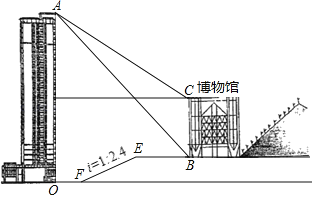
A.10.5B.10.0C.12.0D.12.2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列兩則材料,回答問題:
材料一:平面直角坐標系中,對點A(x1,y1),B(x2,y2)定義一種新的運算:AB=x1x2+y1y2,例如:若A(1,2),B(3,4),則AB=1×3+2×4=11
材料二:平面直角坐標系中,過橫坐標不同的兩點A(x1,y1),B(x2,y2)的直線的斜率為kAB=![]() ,由此可以發現:若kAB=
,由此可以發現:若kAB=![]() =1,則有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,滿足關系式x1﹣y1=x2﹣y2,則有y1﹣y2=x1﹣x2,那么kAB=
=1,則有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,滿足關系式x1﹣y1=x2﹣y2,則有y1﹣y2=x1﹣x2,那么kAB=![]() =1.
=1.
(1)已知點M(﹣2,﹣6),N(3,﹣2),則MN= ,若點A,B的坐標分別為(x1,y1),(x2,y2)(x1≠x2),且滿足關系式2x1+y1=2x2+y2,那么kAB= ;
(2)如圖,橫坐標互不相同的三個點C,D,E滿足CD=DE,且D點是直線y=x上第一象限內的點,點D到原點的距離為2![]() .過點D作DF∥y軸,交直線CE于點F,若DF=6,請結合圖象,求直線CE、直線DF與兩坐標軸圍成的四邊形面積.
.過點D作DF∥y軸,交直線CE于點F,若DF=6,請結合圖象,求直線CE、直線DF與兩坐標軸圍成的四邊形面積.
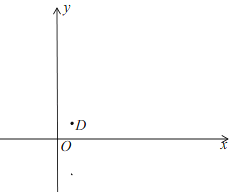
查看答案和解析>>
科目:初中數學 來源: 題型:
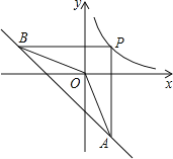
【題目】如圖,P為反比例函數y=![]() (k>0)在第一象限內圖象上的一點,過點P分別作x軸,y軸的垂線交一次函數y=-x-6的圖象于點A、B.若∠AOB=135°,則k的值是______.
(k>0)在第一象限內圖象上的一點,過點P分別作x軸,y軸的垂線交一次函數y=-x-6的圖象于點A、B.若∠AOB=135°,則k的值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中學生騎電動車上學給交通安全帶來隱患,為了解某中學2 500個學生家長對“中學生騎電動車上學”的態度,從中隨機調查400個家長,結果有360個家長持反對態度,則下列說法正確的是( )
A. 調查方式是普查 B. 該校只有360個家長持反對態度
C. 樣本是360個家長 D. 該校約有90%的家長持反對態度
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中有三點(1,2),(3,1),(-2,-1),其中有兩點同時在反比例函數![]() 的圖象上,將這兩點分別記為A,B,另一點記為C,
的圖象上,將這兩點分別記為A,B,另一點記為C,
(1)求出![]() 的值;
的值;
(2)求直線AB對應的一次函數的表達式;
(3)設點C關于直線AB的對稱點為D,P是![]() 軸上的一個動點,直接寫出PC+PD的最小值(不必說明理由).
軸上的一個動點,直接寫出PC+PD的最小值(不必說明理由).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com