
【題目】如圖,已知二次函數的圖像過點![]() ,
,![]() ,與
,與![]() 軸交于另一點
軸交于另一點![]() ,且對稱軸是直線
,且對稱軸是直線![]() .
.
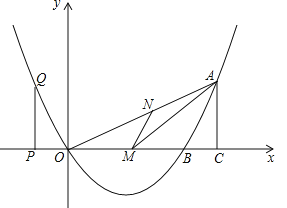
(1)求該二次函數的解析式;
(2)若![]() 是
是![]() 上的一點,作
上的一點,作![]() 交
交![]() 于
于![]() ,當
,當![]() 面積最大時,求
面積最大時,求![]() 的坐標;
的坐標;
(3)![]() 是
是![]() 軸上的點,過
軸上的點,過![]() 作
作![]() 軸,與拋物線交于
軸,與拋物線交于![]() ,過
,過![]() 作
作![]() 軸于
軸于![]() .當以
.當以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 、
、![]() 、
、![]() 為頂點的三角形相似時,求
為頂點的三角形相似時,求![]() 點的坐標.
點的坐標.
【答案】(1)y=![]() x2﹣
x2﹣![]() x;(2)當t=3時,S△AMN有最大值3,此時M點坐標為(3,0);(3)P點坐標為(14,28)或(﹣2,4)或(2,﹣1).
x;(2)當t=3時,S△AMN有最大值3,此時M點坐標為(3,0);(3)P點坐標為(14,28)或(﹣2,4)或(2,﹣1).
【解析】(1)先利用拋物線的對稱性確定B(6,0),然后設交點式求拋物線解析式;
(2)設M(t,0),先其求出直線OA的解析式為y=![]() x,直線AB的解析式為y=2x﹣12,直線MN的解析式為y=2x﹣2t,再通過解方程組
x,直線AB的解析式為y=2x﹣12,直線MN的解析式為y=2x﹣2t,再通過解方程組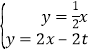 得N(
得N(![]() t,
t,![]() t),接著利用三角形面積公式,利用S△AMN=S△AOM﹣S△NOM得到S△AMN=
t),接著利用三角形面積公式,利用S△AMN=S△AOM﹣S△NOM得到S△AMN=![]() 4t﹣
4t﹣![]() t
t![]() t,然后根據二次函數的性質解決問題;
t,然后根據二次函數的性質解決問題;
(3)設Q(m,![]() m2﹣
m2﹣![]() m),根據相似三角形的判定方法,當
m),根據相似三角形的判定方法,當![]() =
=![]() 時,△PQO∽△COA,則|
時,△PQO∽△COA,則|![]() m2﹣
m2﹣![]() m|=2|m|;當
m|=2|m|;當![]() =
=![]() 時,△PQO∽△CAO,則|
時,△PQO∽△CAO,則|![]() m2﹣
m2﹣![]() m|=
m|=![]() |m|,然后分別解關于m的絕對值方程可得到對應的P點坐標.
|m|,然后分別解關于m的絕對值方程可得到對應的P點坐標.
(1)∵拋物線過原點,對稱軸是直線x=3,
∴B點坐標為(6,0),
設拋物線解析式為y=ax(x﹣6),
把A(8,4)代入得a82=4,解得a=![]() ,
,
∴拋物線解析式為y=![]() x(x﹣6),即y=
x(x﹣6),即y=![]() x2﹣
x2﹣![]() x;
x;
(2)設M(t,0),
易得直線OA的解析式為y=![]() x,
x,
設直線AB的解析式為y=kx+b,
把B(6,0),A(8,4)代入得![]() ,解得
,解得![]() ,
,
∴直線AB的解析式為y=2x﹣12,
∵MN∥AB,
∴設直線MN的解析式為y=2x+n,
把M(t,0)代入得2t+n=0,解得n=﹣2t,
∴直線MN的解析式為y=2x﹣2t,
解方程組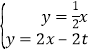 得
得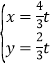 ,則N(
,則N(![]() t,
t,![]() t),
t),
∴S△AMN=S△AOM﹣S△NOM
=![]() 4t﹣
4t﹣![]() t
t![]() t
t
=﹣![]() t2+2t
t2+2t
=﹣![]() (t﹣3)2+3,
(t﹣3)2+3,
當t=3時,S△AMN有最大值3,此時M點坐標為(3,0);
(3)設Q(m,![]() m2﹣
m2﹣![]() m),
m),
∵∠OPQ=∠ACO,
∴當![]() =
=![]() 時,△PQO∽△COA,即
時,△PQO∽△COA,即![]() =
=![]() ,
,
∴PQ=2PO,即|![]() m2﹣
m2﹣![]() m|=2|m|,
m|=2|m|,
解方程![]() m2﹣
m2﹣![]() m=2m得m1=0(舍去),m2=14,此時P點坐標為(14,28);
m=2m得m1=0(舍去),m2=14,此時P點坐標為(14,28);
解方程![]() m2﹣
m2﹣![]() m=﹣2m得m1=0(舍去),m2=﹣2,此時P點坐標為(﹣2,4);
m=﹣2m得m1=0(舍去),m2=﹣2,此時P點坐標為(﹣2,4);
∴當![]() =
=![]() 時,△PQO∽△CAO,即
時,△PQO∽△CAO,即![]() =
=![]() ,
,
∴PQ=![]() PO,即|
PO,即|![]() m2﹣
m2﹣![]() m|=
m|=![]() |m|,
|m|,
解方程![]() m2﹣
m2﹣![]() m=
m=![]() m得m1=0(舍去),m2=8(舍去),
m得m1=0(舍去),m2=8(舍去),
解方程![]() m2﹣
m2﹣![]() m=﹣
m=﹣![]() m得m1=0(舍去),m2=2,此時P點坐標為(2,﹣1);
m得m1=0(舍去),m2=2,此時P點坐標為(2,﹣1);
綜上所述,P點坐標為(14,28)或(﹣2,4)或(2,﹣1).


科目:初中數學 來源: 題型:
【題目】如圖,在邊長為a的正方形的一角剪去一個邊長為b的正方形,把剩余的部分(圖中的陰影部分)裁剪后拼成右邊的長方形.
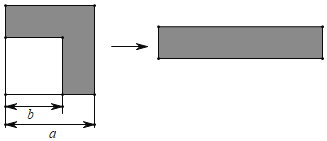
(1)請寫出上述剪拼過程中所揭示的乘法公式;
(2)請運用乘法公式簡便計算:20192﹣2020×2018.
查看答案和解析>>
科目:初中數學 來源: 題型:
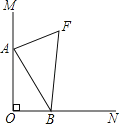
【題目】如圖,∠MON=90°,OB=4,點A是直線OM上的一個動點,連結AB,作∠MAB與∠ABN的角平分線AF與BF,兩條角平分線所在的直線相交于點F,則點A在運動過程中線段BF的最小值為( )
A. 4B. ![]() C. 8D. 2
C. 8D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
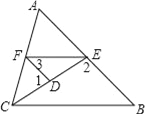
【題目】如圖,已知∠1,∠2互為補角,且∠3=∠B,
(1)求證:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車廠計劃一周生產自行車1400輛,平均每天生產200輛,但由于種種原因,實際每天生產量與計劃量相比有出入,下表是某周的生產情況(超產記為正、減產記為負):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增減產值 |
|
|
|
|
|
|
|
(1)根據記錄的數據可知該廠星期五生產自行車__________輛.
(2)根據記錄的數據可知該廠本周實際生產自行車_________輛.
(3)該廠實行每日計件工資制,每生產一輛車可得60元,若超額完成任務,則超過部分每輛另獎15元,若沒有完成任務,少生產一輛扣20元,那么該廠工人這一周的工作總額是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
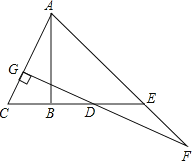
【題目】如圖,AB垂直平分線段CD(AB>CD),點E是線段CD延長線上的一點,且BE=AB,連接AC,過點D作DG⊥AC于點G,交AE的延長線與點F.
(1)若∠CAB=α,則∠AFG= (用α的代數式表示);
(2)線段AC與線段DF相等嗎?為什么?
(3)若CD=6,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是我縣新區部分小區位置簡圖.設港澳城為點A,水榭花都為點B,朝陽家園為點C,濱海華庭為點D,陽光家園為點E,盛世嘉苑為點F,設每個小格的單位為1.
(1)請建立適當的平面直角坐標系,并寫出六個小區的坐標;
(2)依次連接點A、C、E、B,請求出四邊形ACEB的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
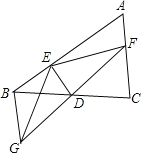
【題目】如圖,△ABC中,D是BC的中點,過D點的直線GF交AC于F,交AC的平行線BG于G點,DE⊥DF,交AB于點E,連結EG、EF.
(1)求證:BG=CF;
(2)請你判斷BE+CF與EF的大小關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com