
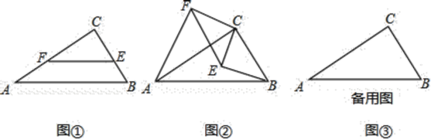
【題目】![]() 嘗試探究:如圖
嘗試探究:如圖![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,E,F分別是BC,AC上的點,且
,E,F分別是BC,AC上的點,且![]() ,則
,則![]() ______;
______;
![]() 類比延伸:如圖
類比延伸:如圖![]() ,若將圖
,若將圖![]() 中的
中的![]() 繞點C順時針旋轉,則在旋轉的過程中,
繞點C順時針旋轉,則在旋轉的過程中,![]() 值是否發生變化?請僅就圖
值是否發生變化?請僅就圖![]() 的情形寫出推理過程;
的情形寫出推理過程;
![]() 拓展運用:若
拓展運用:若![]() ,
,![]() ,在旋轉過程中,當B,E,F三點在同一直線上時,請直接寫出此時線段AF的長.
,在旋轉過程中,當B,E,F三點在同一直線上時,請直接寫出此時線段AF的長.
【答案】(1)![]() ;(2)不變化,理由見解析;(3)AF的長為3
;(2)不變化,理由見解析;(3)AF的長為3![]() -
-![]() 或3
或3![]() +
+![]() .
.
【解析】
(1)根據直角三角形30°角的性質即可解決問題;
(2)只要證明△ACF∽△BCE,可得![]() ,由此即可解決問題;
,由此即可解決問題;
(3)分兩種情形畫出圖形分別解決問題即可;
(1)如圖①中,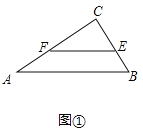
∵在△ABC中,∠ABC=90°,∠A=30°,EF∥AB,
∴∠CFE=∠A=30°,
∴CF=![]() EC,AC=
EC,AC=![]() BC,
BC,
∴AF=AC-CF=![]() BC-
BC-![]() EC=
EC=![]() (BC-EC)=
(BC-EC)=![]() BE,
BE,
∴![]() =
=![]() ,
,
故答案為![]() .
.
(2)不變化,
理由如下:如圖②中,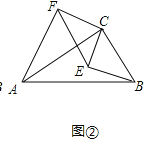
由(1)及旋轉的性質知,∠CFE=∠CAB=30°.
∠FCE=∠ACB=90°.
在Rt△CEF中,tan∠CEF=![]() =
=![]() ,
,
在Rt△CBA中,tan∠ABC=![]() =
=![]() ,
,
∴![]() ,
,
又∵∠FCE=∠ACB=90°,∠FCA+∠ACE=∠FCE,
∠ACE+∠BCE=∠ACB,
∴∠FCA=∠ECB.
∴△ACF∽△BCE,
∴![]() =
=![]() .
.
(3)①如圖,由△ECB∽△FCA,可得:AF:BE=CF:EC=![]() .
.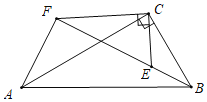
設BE=a,則AF=![]() a,
a,
∵B,E,F共線,
∴∠BEC=∠AFC=120°,
∵∠EFC=30°,
∴∠AFB=90°,
在Rt△ABF中,AB=2BC=6,AF=![]() a,BF=EF+BE=4+a,
a,BF=EF+BE=4+a,
∴(![]() a)2+(4+a)2=62,
a)2+(4+a)2=62,
∴a=-1+![]() 或-1-
或-1-![]() (舍棄),
(舍棄),
∴AF=![]() a=3
a=3![]() -
-![]()
②如圖,當E,B,F共線時,同法可證:AF=![]() BE,∠AFB=90°,
BE,∠AFB=90°,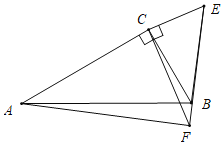
在Rt△ABF中,62=(4-a)2+(![]() a)2,
a)2,
解得a=1+![]() 或1-
或1-![]() (舍棄),
(舍棄),
∴AF=![]() a=3
a=3![]() +
+![]() .
.
AF的長為3![]() -
-![]() 或3
或3![]() +
+![]() .
.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:初中數學 來源: 題型:
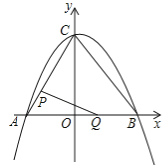
【題目】如圖①,在平面直角坐標系中,二次函數y=![]() x2+bx+c的圖象與坐標軸交于A,B,C三點,其中點A的坐標為(﹣3,0),點B的坐標為(4,0),連接AC,BC.動點P從點A出發,在線段AC上以每秒1個單位長度的速度向點C作勻速運動;同時,動點Q從點O出發,在線段OB上以每秒1個單位長度的速度向點B作勻速運動,當其中一點到達終點時,另一點隨之停止運動,設運動時間為t秒.連接PQ.
x2+bx+c的圖象與坐標軸交于A,B,C三點,其中點A的坐標為(﹣3,0),點B的坐標為(4,0),連接AC,BC.動點P從點A出發,在線段AC上以每秒1個單位長度的速度向點C作勻速運動;同時,動點Q從點O出發,在線段OB上以每秒1個單位長度的速度向點B作勻速運動,當其中一點到達終點時,另一點隨之停止運動,設運動時間為t秒.連接PQ.
(1)填空:b= ,c= ;
(2)在點P,Q運動過程中,△APQ可能是直角三角形嗎?請說明理由;
(3)點M在拋物線上,且△AOM的面積與△AOC的面積相等,求出點M的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在△ABC中,AB=AC=5,BC=6,AD是BC邊上的中線,四邊形ADBE是平行四邊形.
(1)求證:四邊形ADBE是矩形;
(2)求矩形ADBE的面積.
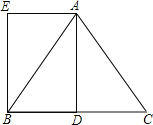
查看答案和解析>>
科目:初中數學 來源: 題型:
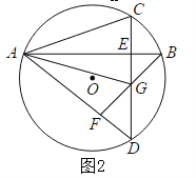
【題目】 AB,CD是![]() 的兩條弦,直線AB,CD互相垂直,垂足為點E,連接AD,過點B作
的兩條弦,直線AB,CD互相垂直,垂足為點E,連接AD,過點B作![]() ,垂足為點F,直線BF交直線CD于點G.
,垂足為點F,直線BF交直線CD于點G.
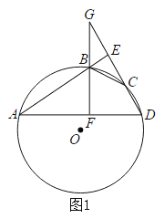
(1)如圖1當點E在![]() 外時,連接
外時,連接![]() ,求證BE平分∠GBC;
,求證BE平分∠GBC;
(2)如圖2當點E在![]() 內時,連接AC,AG,求證:AC=AG
內時,連接AC,AG,求證:AC=AG
(3)在(2)條件下,連接BO,若BO平分![]() ,求線段EC的長.
,求線段EC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,AC=1,記∠ABC=α,點D為射線BC上的動點,連接AD,將射線DA繞點D順時針旋轉α角后得到射線DE,過點A作AD的垂線,與射線DE交于點P,點B關于點D的對稱點為Q,連接PQ.
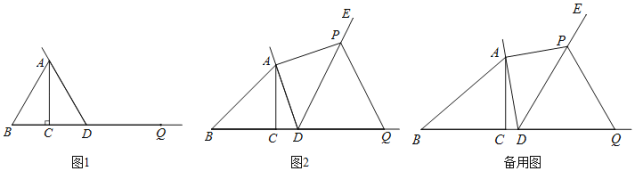
(1)當△ABD為等邊三角形時,
①依題意補全圖1;
②PQ的長為 ;
(2)如圖2,當α=45°,且BD=![]() 時,求證:PD=PQ;
時,求證:PD=PQ;
(3)設BC=t,當PD=PQ時,直接寫出BD的長.(用含t的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
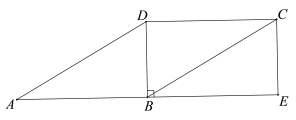
【題目】如圖,在□ABCD中,∠ABD=90°,延長AB至點E,使BE=AB,連接CE.
(1)求證:四邊形BECD是矩形;
(2)連接DE交BC于點F,連接AF,若CE=2,∠DAB=30°,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】M(﹣1,![]() ),N(1,
),N(1,![]() )是平面直角坐標系xOy中的兩點,若平面內直線MN上方的點P滿足:45°≤∠MPN≤90°,則稱點P為線段MN的可視點.
)是平面直角坐標系xOy中的兩點,若平面內直線MN上方的點P滿足:45°≤∠MPN≤90°,則稱點P為線段MN的可視點.
(1)在點![]() ,
,![]() ,
,![]() ,A4(2,2)中,線段MN的可視點為 ;
,A4(2,2)中,線段MN的可視點為 ;
(2)若點B是直線y=x![]() 上線段MN的可視點,求點B的橫坐標t的取值范圍;
上線段MN的可視點,求點B的橫坐標t的取值范圍;
(3)直線y=x+b(b≠0)與x軸交于點C,與y軸交于點D,若線段CD上存在線段MN的可視點,直接寫出b的取值范圍.
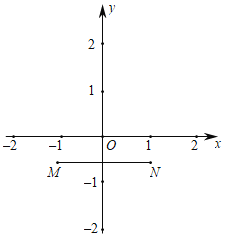
查看答案和解析>>
科目:初中數學 來源: 題型:
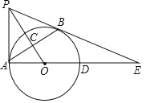
【題目】如圖,PA與⊙O相切于點A,過點A作AB⊥OP,垂足為C,交⊙O于點B.連接PB,AO,并延長AO交⊙O于點D,與PB的延長線交于點E.
(1)求證:PB是⊙O的切線;
(2)若OC=3,AC=4,求PB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
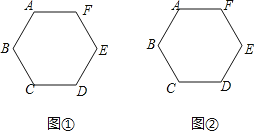
【題目】如圖,已知多邊形ABCDEF中,AB=AF,DC=DE,BC=EF,∠ABC=∠BCD.請僅用無刻度的直尺,分別按下列要求畫圖.
(1)在圖①中,畫出一個以BC為邊的矩形;
(2)在圖②中,若多邊形ABCDEF是正六邊形,試在AF上畫出點M,使得AM=![]() AF.
AF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com