
【題目】如圖1,等邊三角形![]() 中,D為
中,D為![]() 邊上一點,滿足
邊上一點,滿足![]() ,連接
,連接![]() ,以點A為中心,將射線
,以點A為中心,將射線![]() 順時針旋轉(zhuǎn)60°,與
順時針旋轉(zhuǎn)60°,與![]() 的外角平分線
的外角平分線![]() 交于點E.
交于點E.
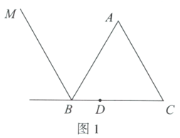
(1)依題意補全圖1;
(2)求證:![]() ;
;
(3)若點B關(guān)于直線![]() 的對稱點為F,連接
的對稱點為F,連接![]() .
.
①求證:![]() ;
;
②若![]() 成立,直接寫出
成立,直接寫出![]() 的度數(shù)為_________°.
的度數(shù)為_________°.
【答案】(1)圖見解析;(2)證明見解析;(3)①證明見解析; ②20°.
【解析】
(1)根據(jù)題意,射線![]() 順時針旋轉(zhuǎn)60°,用尺規(guī)作圖法,做出∠DAE = ∠C = 60°,再連接DE,即完成作圖;
順時針旋轉(zhuǎn)60°,用尺規(guī)作圖法,做出∠DAE = ∠C = 60°,再連接DE,即完成作圖;
(2)在等邊三角形ABC中,由![]() 可得出
可得出![]() ;由射線
;由射線![]() 繞點A順時針旋轉(zhuǎn)60°得到射線
繞點A順時針旋轉(zhuǎn)60°得到射線![]() ,可得∠DAE =
,可得∠DAE =![]() ,進而得出
,進而得出![]() ;由
;由![]() 平分∠ABC的外角
平分∠ABC的外角![]() 可得
可得![]() ,進而推出
,進而推出![]() ,由此可證
,由此可證![]() (ASA),再根據(jù)三角形全等的性質(zhì)易證
(ASA),再根據(jù)三角形全等的性質(zhì)易證![]() ;
;
(3)①連接![]() ,設(shè)
,設(shè)![]() ,根據(jù)點B與點F關(guān)于直線
,根據(jù)點B與點F關(guān)于直線![]() 對稱的性質(zhì)可得
對稱的性質(zhì)可得![]() ,
,![]() ;由
;由![]() 易得
易得![]() ;在等邊三角形
;在等邊三角形![]() 中, 由
中, 由![]() ,
,![]() ,易證
,易證![]() ,
,![]() ,又因為
,又因為![]() ,再根據(jù)三角形AFC的內(nèi)角和定理,可推出
,再根據(jù)三角形AFC的內(nèi)角和定理,可推出![]() ,和前面的證明聯(lián)立可得
,和前面的證明聯(lián)立可得![]() ,所以同旁內(nèi)角互補,
,所以同旁內(nèi)角互補,![]() .
.
②通過圖中各個三角形的內(nèi)角和之間的關(guān)系,設(shè)∠BAD=α,通過證明∠CFA=∠COF推論出![]() ,即可計算出∠BAD=20°.
,即可計算出∠BAD=20°.
(1)依題意補全圖形
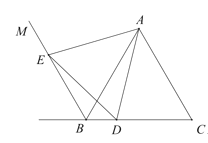
(2)證明:
∵![]() 是等邊三角形,
是等邊三角形,
∴![]() .
.
∴![]() .
.
∵射線![]() 繞點A順時針旋轉(zhuǎn)60°得到射線
繞點A順時針旋轉(zhuǎn)60°得到射線![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.

(3)①證明:連接![]() ,設(shè)
,設(shè)![]() ,
,
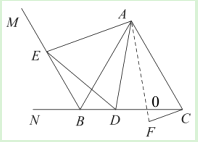
∵點B與點F關(guān)于直線![]() 對稱,
對稱,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵等邊三角形![]() 中,
中,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
且![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
② 由① 知 ![]() ,
,![]()
∴∠EAF=∠F=![]()
∴∠DAF = α,
∵![]() ,由②知BE=CD
,由②知BE=CD
∴BD=CF
∴∠CFA=∠COF
∴![]()
∴3α=60°
∴α=20°


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=-2,與x軸的一個交點在(-3,0)和(-4,0)之間,其部分圖象如圖所示.則下列結(jié)論:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t為實數(shù));⑤點![]() ,
,![]() ,
,![]() 是該拋物線上的點,則y1<y2<y3.其中正確結(jié)論的個數(shù)是( )
是該拋物線上的點,則y1<y2<y3.其中正確結(jié)論的個數(shù)是( )
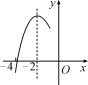
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.
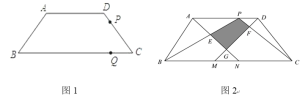
(1)梯形ABCD的面積等于 .
(2)如圖1,動點P從D點出發(fā)沿DC以DC以每秒1個單位的速度向終點C運動,動點Q從C點出發(fā)沿CB以每秒2個單位的速度向B點運動.兩點同時出發(fā),當P點到達C點時,Q點隨之停止運動.當PQ∥AB時,P點離開D點多少時間?
(3)如圖2,點K是線段AD上的點,M、N為邊BC上的點,BM=CN=5,連接AN、DM,分別交BK、CK于點E、F,記△ ADG和△ BKC重疊部分的面積為S,求S的最大值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,正方形
中,正方形![]() 的邊長為2,函數(shù)
的邊長為2,函數(shù)![]() 的圖象經(jīng)過點B,與直線
的圖象經(jīng)過點B,與直線![]() 交于點D.
交于點D.
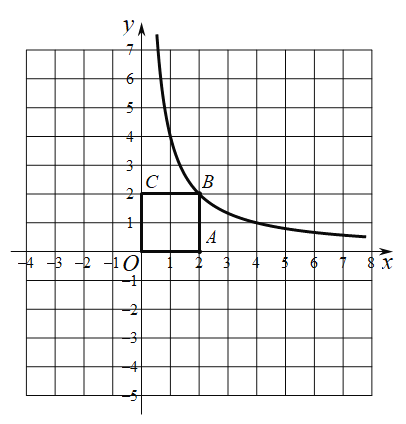
(1)求k的值;
(2)直線![]() 與
與![]() 邊所在直線交于點M,與x軸交于點N.
邊所在直線交于點M,與x軸交于點N.
①當點D為![]() 中點時,求b的值;
中點時,求b的值;
②當![]() 時,結(jié)合函數(shù)圖象,直接寫出b的取值范圍.
時,結(jié)合函數(shù)圖象,直接寫出b的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下面是小王同學“過直線外一點作該直線的平行線”的尺規(guī)作圖過程.
已知:直線l及直線l外一點P.
求作:直線![]() ,使得
,使得![]() .
.

作法:如圖,
①在直線l外取一點A,作射線![]() 與直線l交于點B,
與直線l交于點B,
②以A為圓心,![]() 為半徑畫弧與直線l交于點C,連接
為半徑畫弧與直線l交于點C,連接![]() ,
,
③以A為圓心,![]() 為半徑畫弧與線段
為半徑畫弧與線段![]() 交于點
交于點![]() ,
,
則直線![]() 即為所求.
即為所求.
根據(jù)小王設(shè)計的尺規(guī)作圖過程,,
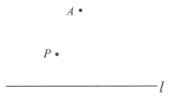
(1)使用直尺和圓規(guī),補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:∵![]() ,
,
∴![]() ,(______________________)(填推理的依據(jù)).
,(______________________)(填推理的依據(jù)).
∵![]() __________,
__________,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() (____________________)(填推理的依據(jù)).
(____________________)(填推理的依據(jù)).
即![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
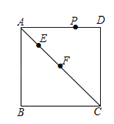
【題目】如圖,在正方形![]() 中,
中,![]() ,
,![]() 、
、![]() 是對角線
是對角線![]() 上的兩個動點(點
上的兩個動點(點![]() 靠近點
靠近點![]() ),且
),且![]() ,
,![]() 是正方形四邊上的任意一點.若
是正方形四邊上的任意一點.若![]() 是等邊三角形,則 AE的長為______ .
是等邊三角形,則 AE的長為______ .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】二次函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() (0,-4)和
(0,-4)和![]() (-2,2).
(-2,2).
(1)求![]() 的值,并用含
的值,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)求證:此拋物線與![]() 軸有兩個不同交點;
軸有兩個不同交點;
(3)當![]() 時,若二次函數(shù)滿足
時,若二次函數(shù)滿足![]() 隨
隨![]() 的增大而減小,求
的增大而減小,求![]() 的取值范圍;
的取值范圍;
(4) 直線![]() 上有一點
上有一點![]() (
(![]() ,5),將點
,5),將點![]() 向右平移4個單位長度,得到點
向右平移4個單位長度,得到點![]() ,若拋物線與線段
,若拋物線與線段![]() 只有一個公共點,求
只有一個公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在邊長為![]() 的正方形ABCD中,點E,F是對角線AC的三等分點,點P在正方形的邊上,則滿足PE+PF=
的正方形ABCD中,點E,F是對角線AC的三等分點,點P在正方形的邊上,則滿足PE+PF=![]() 的點P的個數(shù)是( )
的點P的個數(shù)是( )

A.0B.4C.8D.16
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
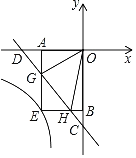
【題目】如圖,在平面直角坐標系xOy中,直線y=﹣x﹣2與x軸,y軸分別交于點D,C.點G,H是線段CD上的兩個動點,且∠GOH=45°,過點G作GA⊥x軸于A,過點H作HB⊥y軸于B,延長AG,BH交于點E,則過點E的反比例函數(shù)y=![]() 的解析式為_____.
的解析式為_____.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com