
【題目】在![]() 中,
中,![]() , 記
, 記![]() ,點
,點![]() 為射線
為射線![]() 上的動點,連接
上的動點,連接![]() ,將射線
,將射線![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 角后得到射線
角后得到射線![]() ,過點
,過點![]() 作
作![]() 的垂線,與射線
的垂線,與射線![]() 交于點
交于點![]() ,點
,點![]() 關于點
關于點![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() .
.
(1)當![]() 為等邊三角形時,
為等邊三角形時,
① 依題意補全圖1;
②![]() 的長為________;
的長為________;
(2)如圖2,當![]() ,且
,且![]() 時, 求證:
時, 求證:![]() ;
;
(3)設![]() , 當
, 當![]() 時,直接寫出
時,直接寫出![]() 的長. (用含
的長. (用含![]() 的代數式表示)
的代數式表示)
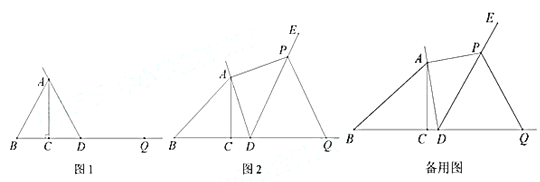
【答案】(1)①見解析,②![]() . (2)見解析;(3)
. (2)見解析;(3)![]() .
.
【解析】
(1)①根據題意補全圖形即可;
②根據旋轉的性質和對稱的性質易證得![]() ,利用特殊角的三角函數值即可求得答案;
,利用特殊角的三角函數值即可求得答案;
(2)作![]() 于
于![]() ,
,![]() 于
于![]() ,證得四邊形
,證得四邊形![]() 是矩形,求得
是矩形,求得![]() ,再證得
,再證得![]() ,求得
,求得![]() ,再求得
,再求得![]() ,即可證得結論.
,即可證得結論.
(3)設![]() 則
則![]() ,證得
,證得![]() ,求得
,求得![]() ,再作DM⊥AB,PN⊥DQ,利用面積法求得
,再作DM⊥AB,PN⊥DQ,利用面積法求得![]() ,繼而求得
,繼而求得![]() ,再證得
,再證得![]() ,求得
,求得![]() ,根據
,根據![]() 得
得![]() ,即可求得答案.
,即可求得答案.
(1)解:①補全圖形如圖所示:
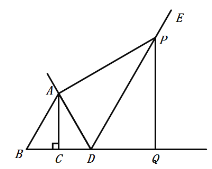
②∵![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,![]() ,
,
根據旋轉的性質和對稱的性質知:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,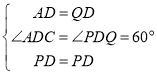 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 為等邊三角形,
為等邊三角形,![]() ,
,
∴ ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
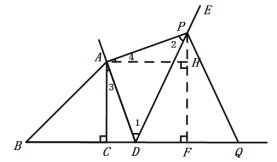
∵![]() ,
,
∴![]() ,
,
由題意可知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四邊形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 關于點
關于點![]() 對稱,
對稱,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 為
為![]() 中點,
中點,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ;
;
(3)∵![]() ,AC⊥BD,
,AC⊥BD,
∴![]() ,
,
設![]() 則
則![]() ,
,
∵AC⊥BD,AP⊥AD,
∴∠ACB=∠PAD![]() ,
,
又∵∠ABC=∠PDA![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴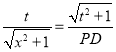 ,
,
∴![]() ,
,
作DM⊥AB,PN⊥DQ,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴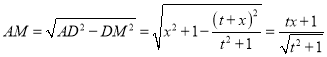 ,
,
∵![]() ,
,
又∵∠AB![]() =∠PDA
=∠PDA![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴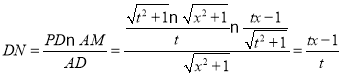 ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.



 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,半徑OC⊥AB于O,AD平分∠CAB交![]() 于點D,連接CD,OD,BD.下列結論中正確的是( )
于點D,連接CD,OD,BD.下列結論中正確的是( )

A.AC∥ODB.![]()
C.△ODE∽△ADOD.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一幅長60 cm、寬40 cm的長方形風景畫的四周鑲一條金色紙邊,制成一幅長方形掛圖,如圖.如果要使整個掛圖的面積是2816 cm2,設金色紙邊的寬為x cm,那么x滿足的方程是( )

A. (60+2x)(40+2x)=2816
B. (60+x)(40+x)=2816
C. (60+2x)(40+x)=2816
D. (60+x)(40+2x)=2816
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象和
的圖象和![]() 軸交于點
軸交于點![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是直線
是直線![]() 上方的拋物線上的動點.
上方的拋物線上的動點.
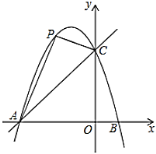
(1)求直線![]() 的解析式.
的解析式.
(2)當![]() 是拋物線頂點時,求
是拋物線頂點時,求![]() 面積.
面積.
(3)在![]() 點運動過程中,求
點運動過程中,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“紅燈停,綠燈行”是我們過路口遇見交通信號燈時必須遵守的規則.小明每天從家騎自行車上學要經過三個路口,假如每個路口交通信號燈中紅燈和綠燈亮的時間相同,且每個路口的交通信號燈只安裝了紅燈和綠燈.那么某天小明從家騎車去學校上學,經過三個路口抬頭看到交通信號燈.
(1)請畫樹狀圖,列舉小明看到交通信號燈可能出現的所有情況;
(2)求小明途經三個路口都遇到紅燈的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
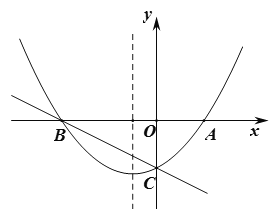
【題目】如圖,對稱軸是![]() 的拋物線
的拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,
,
![]() 求拋物線的函數表達式;
求拋物線的函數表達式;
![]() 若點
若點![]() 是直線
是直線![]() 下方的拋物線上的動點,求
下方的拋物線上的動點,求![]() 的面積的最大值;
的面積的最大值;
![]() 若點
若點![]() 在拋物線對稱軸左側的拋物線上運動,過點
在拋物線對稱軸左側的拋物線上運動,過點![]() 作
作![]() 鈾于點
鈾于點![]() ,交直線
,交直線![]() 于點
于點![]() ,且
,且![]() ,求點
,求點![]() 的坐標;
的坐標;
![]() 在對稱軸上是否存在一點
在對稱軸上是否存在一點![]() ,使
,使![]() 的周長最小,若存在,請求出
的周長最小,若存在,請求出![]() 點的坐標和
點的坐標和![]() 周長的最小值;若不存在,請說明理由.
周長的最小值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com