【題目】已知△ABC，以AB為直徑的⊙O分別交AC于D，BC于E，連接ED，若ED=EC．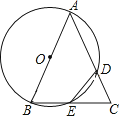
（1）求證：AB=AC；
（2）若AB=4，BC=2 
，求CD的長．
【答案】
（1）
證明：∵ED=EC，
∴∠EDC=∠C，
∵∠EDC=∠B，
∴∠B=∠C，
∴AB=AC
（2）
解：連接AE，
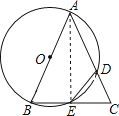
∵AB為直徑，
∴AE⊥BC，
由（1）知AB=AC，
∴BE=CE= 
BC= 
，
∵CECB=CDCA，AC=AB=4，
∴ 2 =4CD，
∴CD= 
【解析】（1）由等腰三角形的性質得到∠EDC=∠C，由圓外接四邊形的性質得到∠EDC=∠B，由此推得∠B=∠C，由等腰三角形的判定即可證得結論；（2）連接AE，由AB為直徑，可證得AE⊥BC，由（1）知AB=AC，由“三線合一”定理得到BE=CE= BC= ，由割線定理可證得結論．本題考查了圓周角定理，等腰三角形的判定和性質，勾股定理，正確的作出輔助線是解題的關鍵．
科目：初中數學 來源： 題型：
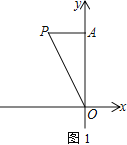
【題目】如圖，平面直角坐標系中，已知點A(0，5)，點P(m，5)在第二象限，連接AP、OP
(1) 如圖1，若OP＝6，求m的值
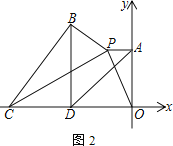
(2) 如圖2，點C在x軸負半軸上，以CP為斜邊作直角三角形BCP，∠CBP＝90°，且∠BPC＝∠APO．取OC的中點D，連接AD、BD，求證：AD＝BD
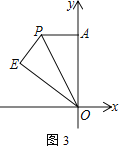
(3) 如圖3，將△AOP沿直線OP翻折得到△EOP（點A的對應點為點E）．若點E到x軸的距離不大于3，直接寫出m的取值范圍（無需解答過程）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，已知直線AB的函數解析式為y=﹣2x+8，與x軸交于點A，與y軸交于點B．
（1）求A、B兩點的坐標；
（2）若點P（m，n）為線段AB上的一個動點（與A、B不重合），作PE⊥x軸于點E，PF⊥y軸于點F，連接EF，問：
①若△PAO的面積為S，求S關于m的函數關系式，并寫出m的取值范圍；
②是否存在點P，使EF的值最小？若存在，求出EF的最小值；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，Rt△AOB中，∠AOB=90°，OA在x軸上，OB在y軸上，點A，B的坐標分別為（ 
，0），（0，1），把Rt△AOB沿著AB對折得到Rt△AO′B，則點O′的坐標為 ．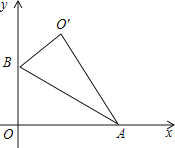 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本小題滿分10分）
如圖，在□ABCD中，以點A為圓心，AB長為半徑畫弧交AD于點F；再分別以點B、F為圓心，大于
BF的相同長為半徑畫弧，兩弧交于點P；連接AP并延長交BC于點E，連接EF，則所得四邊形ABEF是菱形．
（1）根據以上尺規作圖的過程，求證四邊形ABEF是菱形；
（2）若菱形ABEF的周長為16，AE＝4
，求∠C的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某科技館對學生參觀實行優惠，個人票為每張6元，另有團體票可售，票價45元，每票最多限10人入館參觀．
（1）如果參觀的學生人數36人，至少應付多少元？
（2）如果參觀的學生人數為48人，至少應付多少元？
（3）如果參觀的學生人數為一個兩位數
（a表示十位上的數字，b表示個位上的數字），用含a、b的代數式表示至少應付給科技館的總金額．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,已知直線y=-x+2與x軸、y軸分別交于點A和點B,另一直線y=kx+b(k≠0)經過點C(1,0),且把△AOB分成兩部分.
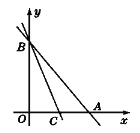
(1)若△AOB被分成的兩部分面積相等,求k和b的值;
(2)若△AOB被分成的兩部分面積比為1∶5,求k和b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
