
【題目】某乒乓球館使用發球機進行輔助訓練,出球口在桌面中線端點A處的正上方,假設每次發出的乒乓球的運動路線固定不變,且落在中線上,在乒乓球運行時,設乒乓球與端點A的水平距離為x(米),與桌面的高度為y(米),經多次測試后,得到如下部分數據:
x/米 | 0 | 0.2 | 0.4 | 0.6 | 1 | 1.4 | 1.6 | 1.8 | … |
y/米 | 0.24 | 0.33 | 0.4 | 0.45 | 0.49 | 0.45 | 0.4 | 0.33 | … |
(1)由表中的數據及函數學習經驗,求出y關于x的函數解析式;
(2)試求出當乒乓球落在桌面時,其落點與端點A的水平距離是多少米?
(3)當乒乓球落在桌面上彈起后,y與x之間滿足![]() .
.
①用含a的代數式表示k;
②已知球網高度為0.14米,球桌長(1.4×2)米.若a=-0.5,那么乒乓球彈起后,是否有機會在某個擊球點可以將球沿直線扣殺到端點A?請說明理由.

【答案】(1)![]() ;(2)乒乓球落在桌面時,落點與端點
;(2)乒乓球落在桌面時,落點與端點![]() 的水平距離是2.4米;(3)①
的水平距離是2.4米;(3)①![]() ;②有機會可以將球沿直線扣殺到端點
;②有機會可以將球沿直線扣殺到端點![]() ,理由詳見解析
,理由詳見解析
【解析】
(1)觀察表格數據發現![]() 是
是![]() 的二次函數,然后利用頂點式,代入系數法求得;
的二次函數,然后利用頂點式,代入系數法求得;
(2)直接令y=0可求得;
(3)①將點![]() 代入
代入![]() ,可得k與
,可得k與![]() 的關系;
的關系;
②先求出扣殺直線的解析式,然后將a=-0.5代入![]() ,與扣殺直線解析式聯立,可求得端點A.
,與扣殺直線解析式聯立,可求得端點A.
解:(1)由表格中數據可判斷,![]() 是
是![]() 的二次函數,且頂點為
的二次函數,且頂點為![]() ,
,
∴設![]() ,
,
將![]() 代入,解得:
代入,解得:![]() ,
,
∴![]() ,
,
(2)由題意,把![]() 代入,有
代入,有![]() ,
,
解得:![]() ,
,![]() (舍去).
(舍去).
∴乒乓球落在桌面時,落點與端點![]() 的水平距離是2.4米.
的水平距離是2.4米.
(3)①由(2)得,乒乓球落在桌面時的坐標為![]() ,
,
將![]() 代入
代入![]() ,解得
,解得![]() ,
,
②∵球網高度為0.14米,端點![]() 到球網的距離為1.4米,
到球網的距離為1.4米,
∴扣殺路線在直線![]() 上,
上,
又∵![]() ,
,
把![]() 代入得
代入得![]() ,
,
∴![]() ,
,
整理得:![]() ,∴
,∴![]() ,
,![]()
∴有機會可以將球沿直線扣殺到端點![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖1,長度為6千米的國道![]() 兩側有
兩側有![]() ,
,![]() 兩個城鎮,從城鎮到公路分別有鄉鎮公路連接,連接點為
兩個城鎮,從城鎮到公路分別有鄉鎮公路連接,連接點為![]() 和
和![]() ,其中
,其中![]() 、
、![]() 之間的距離為2千米,
之間的距離為2千米,![]() 、
、![]() 之間的距離為1千米,
之間的距離為1千米,![]() 、
、![]() 之間的鄉鎮公路長度為2.3千米,
之間的鄉鎮公路長度為2.3千米,![]() 、
、![]() 之間的鄉鎮公路長度為3.2千米,為了發展鄉鎮經濟,方便兩個城鎮的物資輸送,現需要在國道
之間的鄉鎮公路長度為3.2千米,為了發展鄉鎮經濟,方便兩個城鎮的物資輸送,現需要在國道![]() 上修建一個物流基地
上修建一個物流基地![]() ,設
,設![]() 、
、![]() 之間的距離為
之間的距離為![]() 千米,物流基地
千米,物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 兩個城鎮的距離之和為
兩個城鎮的距離之和為![]() 干米,以下是對函數
干米,以下是對函數![]() 隨自變量
隨自變量![]() 的變化規律進行的探究,請補充完整.
的變化規律進行的探究,請補充完整.
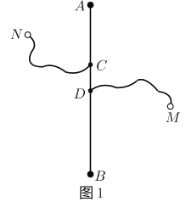
(1)通過取點、畫圖、測量,得到![]() 與
與![]() 的幾組值,如下表:
的幾組值,如下表:
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
(2)如圖2,建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象.
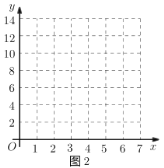
(3)結合畫出的函數圖象,解決問題:
①若要使物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 兩個城鎮的距離之和最小,則物流基地
兩個城鎮的距離之和最小,則物流基地![]() 應該修建在何處?(寫出所有滿足條件的位置)
應該修建在何處?(寫出所有滿足條件的位置)
答:__________.
②如右圖,有四個城鎮![]() 、
、![]() 、
、![]() 、
、![]() 分別位于國道
分別位于國道![]() 兩側,從城鎮到公路分別有鄉鎮公路連接,若要在國道上修建一個物流基地
兩側,從城鎮到公路分別有鄉鎮公路連接,若要在國道上修建一個物流基地![]() ,使得
,使得![]() 沿公路到
沿公路到![]() 、
、![]() 、
、![]() 、
、![]() 的距離之和最小,則物流基地
的距離之和最小,則物流基地![]() 應該修建在何處?(寫出所有滿足條件的位置)
應該修建在何處?(寫出所有滿足條件的位置)
答:__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小區游泳館夏季推出兩種收費方式.方式一:先購買會員證,會員證200元,只限本人當年使用,憑證游泳每次需另付費10元:方式二:不購買會員證,每次游泳需付費20元.
(1)若甲計劃今年夏季游泳的費用為500元,則選擇哪種付費方式游泳次數比較多?
(2)若乙計劃今年夏季游泳的次數超過15次,則選擇哪種付費方式游泳花費比較少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,AB⊥AC,AB=![]() ,BC=
,BC=![]() ,對角線AC,BD相交于點O,將直線AC繞點O順時針旋轉,分別交BC,AD于點E,F,下列說法:①在旋轉過程中,AF=CE. ②OB=AC,③在旋轉過程中,四邊形ABEF的面積為
,對角線AC,BD相交于點O,將直線AC繞點O順時針旋轉,分別交BC,AD于點E,F,下列說法:①在旋轉過程中,AF=CE. ②OB=AC,③在旋轉過程中,四邊形ABEF的面積為![]() ,④當直線AC繞點O順時針旋轉30°時,連接BF,DE則四邊形BEDF是菱形,其中正確的是( )
,④當直線AC繞點O順時針旋轉30°時,連接BF,DE則四邊形BEDF是菱形,其中正確的是( )
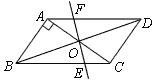
A.①②④B.① ②C.①②③④D.② ③ ④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=![]() x+2與x軸交于點A,與y軸交于點C.拋物線y=ax2+bx+c的對稱軸是x=﹣
x+2與x軸交于點A,與y軸交于點C.拋物線y=ax2+bx+c的對稱軸是x=﹣![]() 且經過A、C兩點,與x軸的另一交點為點B.
且經過A、C兩點,與x軸的另一交點為點B.
(1)①直接寫出點B的坐標;②求拋物線解析式.
(2)若點P為直線AC上方的拋物線上的一點,連接PA,PC.求△PAC的面積的最大值,并求出此時點P的坐標.
(3)拋物線上有一點M,過點M作MN垂直x軸于點N,使得以點A、M、N為頂點的三角形與△ABC相似,直接寫出點M的坐標.
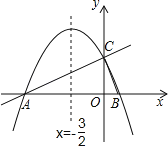
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的一條弦,點C在半徑OA上且不與點A,O重合,過點C作CD⊥OA于點C,交弦AB于點E,交過點B的⊙O的切線于點D.
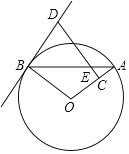
(1)求證:DB=DE;
(2)若sin∠ABO=![]() ,BE=10,求DE的長.
,BE=10,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=-x2+bx+c經過點A(3,0)和點B(2,3),過點A的直線與y軸的負半軸相交于點C,且tan∠CAO=![]() .
.
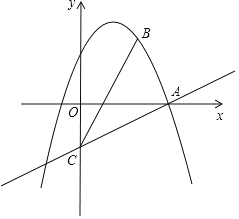
(1)求這條拋物線的表達式及對稱軸;
(2)聯結AB、BC,求∠ABC的正切值;
(3)若點D在x軸下方的對稱軸上,當S△DBC=S△ADC時,求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】參照學習函數的過程方法,探究函數![]() 的圖像與性質,因為
的圖像與性質,因為![]() ,即
,即![]() ,所以我們對比函數
,所以我們對比函數![]() 來探究列表:
來探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描點:在平面直角坐標系中以自變量![]() 的取值為橫坐標,以
的取值為橫坐標,以![]() 相應的函數值為縱坐標,描出相應的點如圖所示:
相應的函數值為縱坐標,描出相應的點如圖所示:
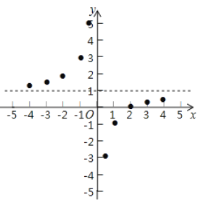
(1)請把![]() 軸左邊各點和右邊各點分別用一條光滑曲線,順次連接起來;
軸左邊各點和右邊各點分別用一條光滑曲線,順次連接起來;
(2)觀察圖象并分析表格,回答下列問題:
①當![]() 時,
時,![]() 隨
隨![]() 的增大而______;(“增大”或“減小”)
的增大而______;(“增大”或“減小”)
②![]() 的圖象是由
的圖象是由![]() 的圖象向______平移______個單位而得到的;
的圖象向______平移______個單位而得到的;
③圖象關于點______中心對稱.(填點的坐標)
(3)函數![]() 與直線
與直線![]() 交于點
交于點![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖菱形![]() 中,
中,![]() ,點C坐標
,點C坐標![]() ,過點
,過點![]() 作直線
作直線![]() 分別交
分別交![]() 于點
于點![]() ,交
,交![]() 于E,點E在反比例函數
于E,點E在反比例函數![]() 的圖象上,若
的圖象上,若![]() 和
和![]() (即圖中兩陰影部分)的面積相等,則
(即圖中兩陰影部分)的面積相等,則![]() 的值為_______.
的值為_______.
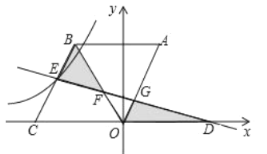
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com