
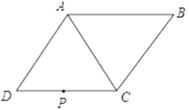
【題目】如圖,在菱形ABCD中,∠ADC=60°,CD=4![]() cm,P為CD的中點.
cm,P為CD的中點.
(1)在AC上找一點Q,使DQ+PQ的值最小(保留畫圖痕跡,不寫畫法,不必說理);
(2)求出(1)中DQ+PQ的長.
【答案】(1)見解析;(2)2![]() cm
cm
【解析】
(1)如圖,連接 PB 交 AC 于點 Q,點 Q 是所求作的;
(2)連接 PA.證明△PAB 是直角三角形,利用勾股定理求出 PB 即可;
解:(1)如圖,連接 PB 交 AC 于點 Q,點 Q 是所求作的;
(2)連結 AP,

在菱形 ABCD 中,AB=AD=CD=4![]() cm,又∵∠ADC=60°,
cm,又∵∠ADC=60°,
∴△ACD 為等邊三角形,
∵P 為 CD 的中點,
AP⊥CD,DP= ![]() CD=2
CD=2![]() cm, 在 Rt△ADP 中,
cm, 在 Rt△ADP 中,
∴AP=![]()
![]() =6(cm),
=6(cm),
∵AP⊥CD,AB∥CD,
∴AP⊥AB,
在 Rt△ABP 中,BP=![]() =
=![]() (cm),
(cm),
在菱形 ABCD 中,AC⊥BD,OB=OD
∴DQ=BQ
∴DQ+PQ=BQ+PQ=BP=2![]() (cm).
(cm).
答:DQ+PQ 的長為 2![]() cm.
cm.


科目:初中數學 來源: 題型:
【題目】如圖1,已知二次函數![]() (
(![]() 為常數,
為常數,![]() )的圖象過點
)的圖象過點![]() 和點
和點![]() ,函數圖象最低點
,函數圖象最低點![]() 的縱坐標為
的縱坐標為![]() .直線
.直線![]() 的解析式為
的解析式為![]()
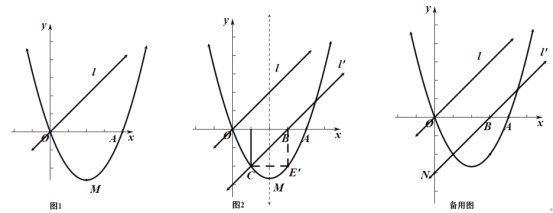
![]() 求二次函數的解析式;
求二次函數的解析式;
![]() 直線
直線![]() 沿
沿![]() 軸向右平移,得直線
軸向右平移,得直線![]() ,
,![]() 與線段
與線段![]() 相交于點
相交于點![]() ,與
,與![]() 軸下方的拋物線相交于點
軸下方的拋物線相交于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,把
,把![]() 沿直線
沿直線![]() 折疊,當點
折疊,當點![]() 恰好落在拋物線上點
恰好落在拋物線上點![]() 時(圖
時(圖![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 在
在![]() 的條件下,
的條件下,![]() 與
與![]() 軸交于點
軸交于點![]() ,把
,把![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,P為
,P為![]() 上的動點,當
上的動點,當![]() 為等腰三角形時,求符合條件的點
為等腰三角形時,求符合條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,以Rt△ABC的斜邊BC為一邊在△ABC的同側作正方形BCEF,設正方形的中心為O,連接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
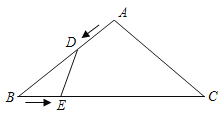
【題目】如圖所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.點D由點A出發沿AB方向向點B勻速運動,同時點E由點B出發沿BC方向向點C勻速運動,它們的速度均為1cm/s.連接DE,設運動時間為t(s)(0<t<10),解答下列問題:
(1)當t為何值時,△BDE的面積為7.5cm2;
(2)在點D,E的運動中,是否存在時間t,使得△BDE與△ABC相似?若存在,請求出對應的時間t;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() .
.![]() 于
于![]() .
.![]() 為邊
為邊![]() 上的一個(不與
上的一個(不與![]() 、
、![]() 重合)點,且
重合)點,且![]() 于
于![]() 相交于點
相交于點![]() .
.

(1)填空:![]() ______;
______;![]() ______.
______.
(2)當![]() 時,證明:
時,證明:![]() .
.
(3)![]() 面積的最小值是_______.
面積的最小值是_______.
(4)當![]() 的內心在
的內心在![]() 的外部時,直接寫出
的外部時,直接寫出![]() 的范圍______.
的范圍______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義一種對正整數n的“F”運算:①當n為奇數時,F(n)=3n+1;②當n為偶數時,F(n)=![]() (其中k是使F(n)為奇數的正整數)……,兩種運算交替重復進行,例如,取n=24,則:
(其中k是使F(n)為奇數的正整數)……,兩種運算交替重復進行,例如,取n=24,則:

若n=24,則第2019次“F”運算的結果是( )
A.4B.1C.2018D.42018
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件8元,出廠價為每件10元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=-10x+500.
(1)李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3410元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,矩形ABCD中,AB=5,BC=8,點P為BC上一動點(不與端點重合),連接AP,將△ABP沿著AP折疊.點B落到M處,連接BM、CM,若△BMC為等腰三角形,則BP的長度為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵城市周邊的農民的種菜的積極性,某公司計劃新建![]() ,
,![]() 兩種溫室80棟,將其售給農民種菜.已知建1個
兩種溫室80棟,將其售給農民種菜.已知建1個![]() 型溫室和2個
型溫室和2個![]() 型溫室一共需要8.1萬元,兩種溫室的成本和出售價如下表:
型溫室一共需要8.1萬元,兩種溫室的成本和出售價如下表:
|
| |
成本(萬元/棟) | 2.5 |
|
出售價(萬元/棟) | 3.1 | 3.5 |
(1)求![]() 的值;
的值;
(2)已知新建![]() 型溫室不少于38棟不多于50棟且所建的兩種溫室可全部售出.為了減輕菜農負擔,試問采用什么方案建設溫室可使利潤最少,最少利潤是多少?
型溫室不少于38棟不多于50棟且所建的兩種溫室可全部售出.為了減輕菜農負擔,試問采用什么方案建設溫室可使利潤最少,最少利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com