
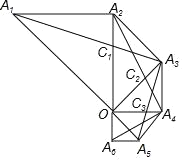
【題目】如圖,面積為1的等腰直角△OA1A2,∠OA2A1=90°,以OA2為斜邊在△OA1A2外部作等腰直角△OA2A3,以OA3為斜邊在△OA2A3外部作等腰直角△OA3A4,以OA4為斜邊在△OA3A4外部作等腰直角△OA4A5,…,連接A1A3,A2A4,A3A5,…分別與OA2,OA3,OA4,交于點C1,C2,C3,按此規律繼續下去,則△OAnCn的面積等于_____.(用含正整數n的式子表示)
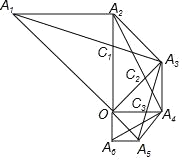
【答案】![]()
【解析】
根據題意做等腰直角三角形,可由第一個直角邊為1推出之后的面積及直角邊長度,A2A3的長為1,△OA2A3的面積為![]() ,A3A4的長為
,A3A4的長為![]()
![]() ,△OA3A4的面積為
,△OA3A4的面積為![]() ,以此類推,AnAn+1的長為
,以此類推,AnAn+1的長為![]() ,△OAnAn+1的面積為
,△OAnAn+1的面積為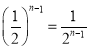 ,又可知△A1OC1∽△A3A2C1,即
,又可知△A1OC1∽△A3A2C1,即![]() =
=![]() ,即S△A1OC1=
,即S△A1OC1=![]() S△A1OA2=
S△A1OA2=![]() ,同理可得,S△A2OC2=
,同理可得,S△A2OC2=![]() S△A2OA3=
S△A2OA3=![]() ×
×![]() =
=![]() ,以此類推,S△AnOCn=
,以此類推,S△AnOCn=![]() S△AnOAn+1=
S△AnOAn+1=![]() ×
×![]() =
=![]() ,
,
解:∵面積為1的等腰直角△OA1A2,∠OA2A1=90°,
∴A1A2=![]() ,OA1=2,
,OA1=2,
∵以OA2為斜邊在△OA1A2外部作等腰直角△OA2A3,
∴A2A3的長為1,△OA2A3的面積為![]() ,
,
∵以OA3為斜邊在△OA2A3外部作等腰直角△OA3A4,
∴A3A4的長為![]()
![]() ,△OA3A4的面積為
,△OA3A4的面積為![]() ,
,
以此類推,AnAn+1的長為![]() ,△OAnAn+1的面積為
,△OAnAn+1的面積為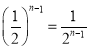 ,
,
∵A1O∥A2A3,
∴△A1OC1∽△A3A2C1,
∴![]() =
=![]() ,即S△A1OC1=
,即S△A1OC1=![]() S△A1OA2=
S△A1OA2=![]() ,
,
同理可得,S△A2OC2=![]() S△A2OA3=
S△A2OA3=![]() ×
×![]() =
=![]() ,
,
…
以此類推,S△AnOCn=![]() S△AnOAn+1=
S△AnOAn+1=![]() ×
×![]() =
=![]() ,
,
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】在2018年“新技術支持未來教育”的教師培訓活動中,會議就“面向未來的學校教育、家庭教育及實踐應用演示”等問題進行了互動交流,記者隨機采訪了部分參會教師,對他們發言的次數進行了統計,并繪制了不完整的統計表和條形統計圖.
組別 | 發言次數n | 百分比 |
A | 0≤n<3 | 10% |
B | 3≤n<6 | 20% |
C | 6≤n<9 | 25% |
D | 9≤n<12 | 30% |
E | 12≤n<15 | 10% |
F | 15≤n<18 | m% |
請你根據所給的相關信息,解答下列問題:
(1)本次共隨機采訪了 _____ 名教師,m= _____ ;
(2)補全條形統計圖;
(3)已知受訪的教師中,E組只有2名女教師,F組恰有1名男教師,現要從E組、F組中分別選派1名教師寫總結報告,請用列表法或畫樹狀圖的方法,求所選派的兩名教師恰好是1男1女的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
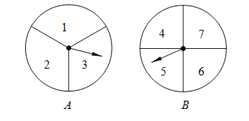
【題目】甲、乙兩人用如圖的兩個分格均勻的轉盤A、B做游戲,游戲規則如下:分別轉動兩個轉盤,轉盤停止后,指針分別指向一個數字(若指針停止在等份線上,那么重轉一次,直到指針指向某一數字為止).用所指的兩個數字相乘,如果積是奇數,則甲獲勝;如果積是偶數,則乙獲勝.請你解決下列問題:
(1)用列表格或畫樹狀圖的方法表示游戲所有可能出現的結果.
(2)求甲、乙兩人獲勝的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
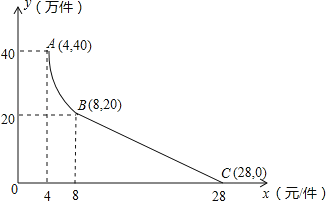
【題目】某公司用100萬元研發一種市場急需電子產品,已于當年投入生產并銷售,已知生產這種電子產品的成本為4元/件,在銷售過程中發現:每年的年銷售量y(萬件)與銷售價格x(元/件)的關系如圖所示,其中AB為反比例函數圖象的一部分,設公司銷售這種電子產品的年利潤為s(萬元).
(1)請求出y(萬件)與x(元/件)的函數表達式;
(2)求出第一年這種電子產品的年利潤s(萬元)與x(元/件)的函數表達式,并求出第一年年利潤的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
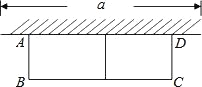
【題目】如圖,有長為 24m 的籬笆,現一面利用墻(墻的最大可用長度 a 為 10m)圍成中間隔有一道籬笆的長方形花圃,設花圃的寬 AB 為 xm,面積為 Sm2.
(1) 求 S 與 x 的函數關系式及 x 值的取值范圍;
(2) 要圍成面積為 45m2 的花圃,AB 的長是多少米?
(3) 當 AB 的長是多少米時,圍成的花圃的面積最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
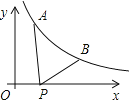
【題目】如圖所示,已知A(![]() ,y1),B(2,y2)為反比例函數
,y1),B(2,y2)為反比例函數![]() 圖像上的兩點,動點P(x,0)在x正半軸上運動,當線段AP與線段BP之差達到最大時,點P的坐標是( )
圖像上的兩點,動點P(x,0)在x正半軸上運動,當線段AP與線段BP之差達到最大時,點P的坐標是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
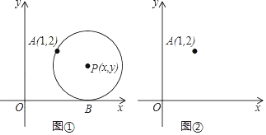
【題目】如圖①,在平面直角坐標系中,圓心為P(x,y)的動圓經過點A(1,2)且與x軸相切于點B.
(1)當x=2時,求⊙P的半徑;
(2)求y關于x的函數解析式;判斷此函數圖象的形狀;并在圖②中畫出此函數的圖象;
(3)當⊙P的半徑為1時,若⊙P與以上(2)中所得函數圖象相交于點C、D,其中交點D(m,n)在點C的右側,請利用圖②,求cos∠APD的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
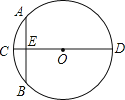
【題目】“圓材埋壁”是我國古代數一學著作《九章算術》中的一個問題.“今有圓材,埋壁中,不知大小,以鋸鋸之,深一寸,鋸道長一尺,問徑幾何?”用現在的數學語言表達是:如圖所示,CD為⊙O的直徑,弦AB⊥CD,垂足為E,CE=1寸,AB=1尺,則直徑CD長為_____寸.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2-2(m+1)x+2m+1(m為常數),函數圖像的頂點為C.
(1)若該函數的圖像恰好經過坐標原點,求點C的坐標;
(2)該函數的圖像與x軸分別交于點A、B,若以A、B、C為頂點的三角形是直角三角形,求m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com