【題目】（1）如圖，∠1＝75°，∠2＝105°，∠C＝∠D．判斷 ∠A與 ∠F的大小關系，并說明理由．
（2）對于某些數學問題，靈活運用整體思想，可以化難為易．在解二元一次方程組時，就可以運用整體代入法：如解方程組：
.
解：把②代入①得，
解得
把
代入②得，
所以方程組的解為 
請用同樣的方法解方程組：
.
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
快樂暑假暑假能力自測中西書局系列答案科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程(a+b)x2+2cx+(b-a)=0，其中a、b、c分別為
三邊的長.
(1)如果
是方程的根，試判斷
的形狀，并說明理由.
(2)如果方程有兩個相等的實數根，試判斷
的形狀，并說明理由.
(3)如果
是等邊三角形，試求這個一元二次方程的根.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與實踐
問題情境：如圖1，在正方形
中，點
是對角線
上的一點，點
在
的延長線上，且
，
交
于點
．問題解決：
（1）求證：
；
（2）求
的度數；
探索發現：
（3）如圖2，若點在邊上，且，求的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，AO是△ABC的角平分線．以O為圓心，OC為半徑作⊙O．
（1）求證：AB是⊙O的切線．
（2）已知AO交⊙O于點E，延長AO交⊙O于點D，tanD=
，求
的值．
（3）（3分）在（2）的條件下，設⊙O的半徑為3，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知
，
，
，點E在線段AB上，
，點F在直線AD上，
．
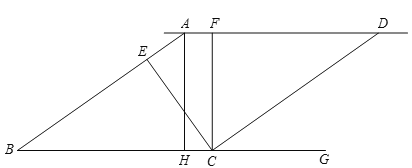
若
，求
的度數；
找出圖中與
相等的角，并說明理由；
在
的條件下，點
不與點B、H重合
從點B出發，沿射線BG的方向移動，其他條件不變，請直接寫出
的度數
不必說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在
的正方形網格中，從點
出發的四條線段
，
，
，
，它的另一個端點
，
，
，
均在格點上（正方形網格的交點）．
（1）若每個小正方形的邊長都是1，分別求出，，，的長度（結果保留根號）．
（2）在，，，四條線段中，是否存在三條線段，它們能構成直角三角形？如果存在，請指出是哪三條線段，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
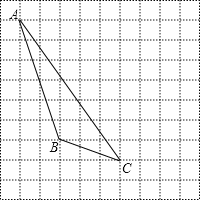
【題目】如圖,每個小正方形的邊長為1個單位,每個小方格的頂點叫格點．
(1)畫出△ABC的AB邊上的中線CD;
(2)畫出△ABC向右平移4個單位后得到的△A1B1C1;
(3)圖中AC與A1C1的關系是： ;
(4)能使S △ABQ=S △ABC的格點Q,共有 個,在圖中分別用Q 1,Q 2,…表示出來．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點A（m，n）在第一象限內，m，n均為整數，且滿足
.
（1）求點A的坐標；
（2）將線段OA向下平移a（a>0）個單位后得到線段
，過點
作
軸于點B，若
，求a的值；
（3）過點A向x軸作垂線，垂足為點C，點M從O出發，沿y軸的正半軸以每秒2個單位長度的速度運動，點N從點C出發，以每秒3個單位長度的速度向x軸負方向運動，點M與點N同時出發，設點M的運動時間為t秒，當
時，判斷四邊形AMON的面積
的值是否變化？若不變，求出其值；若變化，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在平面直角坐標系中，A、B為x軸上兩點，C、D為y軸上兩點，經過點A，C，B的拋物線的一部分C1與經過點A，D，B的拋物線的一部分C2組合成一條封閉曲線，我們把這條封閉曲線稱為“蛋線”．已知點C的坐標為（0， 
），點M是拋物線C2：y=mx2-2mx-3m（m＜0）的頂點：
（1）求A、B兩點的坐標；
（2）求經過點A，C，B的拋物線C1的函數表達式．
（3）探究“蛋線”在第四象限上是否存在一點P，使得△PBC的面積最大？若存在，求出點P的坐標及△PBC面積的最大值；若不存在，請說明理由．
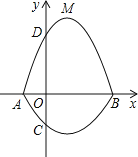
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
