
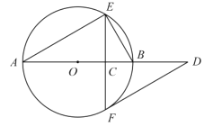
【題目】如圖,![]() 是
是![]() 的直徑,弦
的直徑,弦![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 的切線交
的切線交![]() 的延長線于點
的延長線于點![]() .
.
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
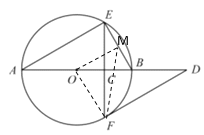
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,請補全圖形;若
,請補全圖形;若![]() ,
,![]() ,求
,求![]() 的半徑.
的半徑.
【答案】(1)![]() =
=![]() ;(2)
;(2)![]() 的半徑為4.
的半徑為4.
【解析】
(1)連接OF,求出∠BOF=2∠A=![]() ,利用DF是
,利用DF是![]() 的切線證得∠CFD=∠COF=
的切線證得∠CFD=∠COF=![]() 即可得到答案;
即可得到答案;
(2)如圖,連接OM,根據M是BE的中點,O是AB的中點求出∠MOB=![]() ,∠OMB=90°,設
,∠OMB=90°,設![]() 的半徑為r得到OM=
的半徑為r得到OM=![]() ,根據勾股定理得到
,根據勾股定理得到![]() ,求出r即可.
,求出r即可.
(1)連接OF,
∵![]() 是
是![]() 的直徑,弦
的直徑,弦![]() 于點
于點![]() ,
,
∴![]() ,∠ACE=∠ACF=90°,
,∠ACE=∠ACF=90°,
∴∠BOF=2∠A=![]() ,∠OFC+∠COF=90°,
,∠OFC+∠COF=90°,
∵DF是![]() 的切線,
的切線,
∴∠OFD=90°,
∴∠OFC+∠CFD=90°,
∴∠CFD=∠COF=![]() ,
,
即![]() =
=![]() ;
;

(2)如圖,連接OM,
∵M是BE的中點,O是AB的中點,
∴OM∥AE,
∠MOB=![]() ,∠OMB=90°,
,∠OMB=90°,
設![]() 的半徑為r,
的半徑為r,
∴OM=![]() ,
,
∵∠BOF=2∠A=60°,
∴∠MOF=90°,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得r=4,
∴![]() 的半徑為4.
的半徑為4.


科目:初中數學 來源: 題型:
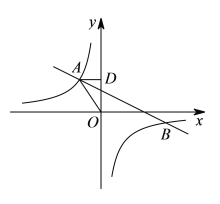
【題目】如圖,在平面直角坐標系中,反比例函數![]()
![]() 與一次函數
與一次函數![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
(1)求反比例函數和一次函數的解析式;
(2)請根據圖象直接寫出![]() 的自變量
的自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等腰直角![]() 中,
中,![]() ,點
,點![]() 是
是![]() 邊上一點,以
邊上一點,以![]() 為邊作等腰直角
為邊作等腰直角![]() ,其中
,其中![]() ,邊
,邊![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 是
是![]() 上一點.
上一點.
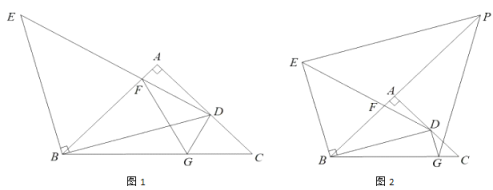
(1)如圖1,若![]() ,連接
,連接![]() .
.
①若![]() ,求
,求![]() 的長度;
的長度;
②求證:![]() ;
;
(2)如圖2,若![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,請猜想線段
,請猜想線段![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 中,對角線
中,對角線![]() 交于點
交于點![]() ,折疊正方形紙片,使
,折疊正方形紙片,使![]() 落在
落在![]() 上,點
上,點![]() 恰好與
恰好與![]() 上的點
上的點![]() 重合,展開后折痕
重合,展開后折痕![]() 分別交
分別交![]() 于點
于點![]() ,連
,連![]() 給出下列結論,其中正確的個數有( )
給出下列結論,其中正確的個數有( )
①![]() ;②
;②![]() ;③四邊形
;③四邊形![]() 是菱形;④
是菱形;④![]() .
.
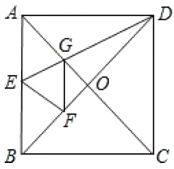
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
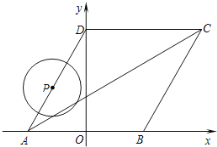
【題目】如圖所示,菱形ABCD的頂點A、B在![]() 軸上,點A在點B的左側,點D在
軸上,點A在點B的左側,點D在![]() 軸的正半軸上,
軸的正半軸上,![]() ,點A的坐標為
,點A的坐標為![]() .
.
(1)求D點的坐標.
(2)求直線AC的函數關系式.
(3)動點P從點A出發,以每秒1個單位長度的速度,按照![]() 的順序在菱形的邊上勻速運動一周,設運動時間為
的順序在菱形的邊上勻速運動一周,設運動時間為![]() 秒.求
秒.求![]() 為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
查看答案和解析>>
科目:初中數學 來源: 題型:
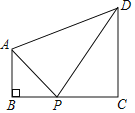
【題目】如圖,四邊形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=m,點P是邊BC上一動點,若△PAB與△PCD相似,且滿足條件的點P恰有2個,則m的值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
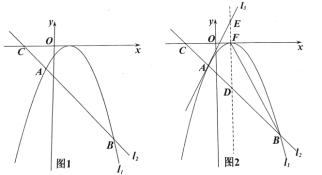
【題目】如圖1,拋物線![]() 與直線
與直線![]() (
(![]() 為常數
為常數![]() ,)交于A,B兩點,直線
,)交于A,B兩點,直線![]() 交
交![]() 軸于點C,點A的坐標為
軸于點C,點A的坐標為![]() ;
;
(1)若![]() ,則A點的坐標為__________,點B的坐標為____________
,則A點的坐標為__________,點B的坐標為____________
(2)已知點![]() ,拋物線
,拋物線![]() 與線段
與線段![]() 有兩個公共點,求
有兩個公共點,求![]() 的取值范圍;
的取值范圍;
(3)①如圖1,求證: ![]()
②如圖2,設拋物線的頂點為F,直線![]() 交拋物線的對稱軸于點
交拋物線的對稱軸于點![]() ,直線
,直線![]() (
(![]() 為常數
為常數![]() ,)經過點A,并交拋物線的對稱軸于點E,若
,)經過點A,并交拋物線的對稱軸于點E,若![]() (
(![]() 為常數)則
為常數)則![]() 的值是否發生變化?若不變,請求出
的值是否發生變化?若不變,請求出![]() 的值;若變化,請說明理由.
的值;若變化,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人相約周末登花果山,甲、乙兩人距地面的高度![]() (米)與登山時間
(米)與登山時間![]() (分)之間的函數圖象如圖所示,根據圖象所提供的信息解答下列問題:
(分)之間的函數圖象如圖所示,根據圖象所提供的信息解答下列問題:
(1)甲登山上升的速度是每分鐘 米,乙在![]() 地時距地面的高度
地時距地面的高度![]() 為 米;
為 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,請求出乙登山全程中,距地面的高度![]() (米)與登山時間
(米)與登山時間![]() (分)之間的函數關系式.
(分)之間的函數關系式.
(3)登山多長時間時,甲、乙兩人距地面的高度差為50米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某新建火車站站前廣場需要綠化的面積為46000米2,施工隊在綠化了22000米2后,將每天的工作量增加為原來的1.5倍,結果提前4天完成了該項綠化工程.
(1)該項綠化工程原計劃每天完成多少米2?
(2)該項綠化工程中有一塊長為20米,寬為8米的矩形空地,計劃在其中修建兩塊相同的矩形綠地,它們的面積之和為56米2,兩塊綠地之間及周邊留有寬度相等的人行通道(如圖所示),問人行通道的寬度是多少米?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com