
【題目】在“全民讀書月”活動中,小明調查了班級里40名同學本學期購買課外書的費用情況,并將結果繪制成如圖所示的統計表和扇形統計圖,請根據相關信息,解答下列問題:(直接填寫結果)
費用(元) | 20 | 30 | 50 | 80 | 100 |
人數 | 6 | a | 10 | b | 4 |
(1)本次調查獲取的樣本數據的眾數是 元,中位數是 元;
(2)扇形統計圖中,“50元”所對應的圓心角的度數為 度,該班學生購買課外書的平均費用為 元;
(3)若該校共有學生1000人,根據樣本數據,估計本學期購買課外書花費50元的學生有 人.
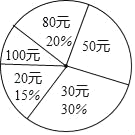
【答案】(1)30,50;(2)90,50.5;(3)250.
【解析】
(1)眾數就是出現次數最多的數,據此即可判斷;中位數就是大小處于中間位置的數,根據定義判斷;
(2)根據題意列出算式,求出即可;
(3)利用1000乘以本學期計劃購買課外書花費50元的學生所占的比例即可求解.
解:(1)∵a=40×30%=12,b=40×20%=8,
∴眾數是:30元,中位數是:50元;
故答案是:30,50;
(2)圓心角的度數為:360°×![]() =90°,
=90°,
![]() ×(6×20+12×30+10×50+8×80+4×100)=50.5(元),
×(6×20+12×30+10×50+8×80+4×100)=50.5(元),
故答案為50.5;
(3)調查的總人數是:6+12+10+8+4=40(人),
則估計本學期計劃購買課外書花費50元的學生有:1000×![]() =250(人).
=250(人).
故答案是:250.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】據調查,超速行駛是引發交通事故的主要原因之一,所以規定以下情境中的速度不得超過15m/s在一條筆直公路BD的上方A處有一探測儀,如平面幾何圖,AD=24m,∠D=90°,第一次探測到一輛轎車從B點勻速向D點行駛,測得∠ABD=31°,2秒后到達C點,測得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,結果精確到1m).
(1)求B,C的距離.
(2)通過計算,判斷此轎車是否超速.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從甲、乙兩位運動員中選出一名參加在規定時間內的投籃比賽.預先對這兩名運動員進行了6次測試,成績如下(單位:個):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均數 | 眾數 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根據測試成績,請你運用所學的統計知識作出分析,派哪一位運動員參賽更好?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
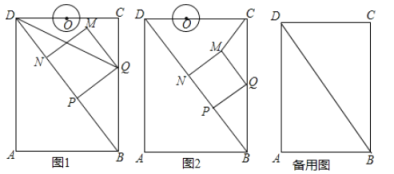
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 從點
從點![]() 出發,沿對角線
出發,沿對角線![]() 向點
向點![]() 勻速運動,速度為
勻速運動,速度為![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,以
,以![]() 為一邊作正方形
為一邊作正方形![]() ,使得點
,使得點![]() 落在射線
落在射線![]() 上.點
上.點![]() 從點
從點![]() 出發,沿
出發,沿![]() 向點
向點![]() 勻速運動,速度為
勻速運動,速度為![]() ,以
,以![]() 為圓心,
為圓心,![]() 半徑作
半徑作![]() .點
.點![]() 與點
與點![]() 同時出發,設它們的運動時間為
同時出發,設它們的運動時間為![]() (單位:
(單位:![]() )
)![]() .
.
(1)如圖1,連接![]() ,若
,若![]() 平分
平分![]() ,則
,則![]() 的值為__________
的值為__________![]() ;
;
(2)如圖2,連接![]() ,設
,設![]() 的面積為
的面積為![]() ,求
,求![]() 關于t的函數關系式;
關于t的函數關系式;
(3)在運動過程中,當![]() 為何值時,
為何值時,![]() 與
與![]() 第一次相切?
第一次相切?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中有兩點![]() 、
、![]() ,我們定義
,我們定義![]() 、
、![]() 兩點間的“
兩點間的“![]() 值”直角距離為
值”直角距離為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() .小靜和佳佳在解決問題:(求點
.小靜和佳佳在解決問題:(求點![]() 與點
與點![]() 的“1值”直角距離
的“1值”直角距離![]() )時,采用了兩種不同的方法:
)時,采用了兩種不同的方法:
(方法一):![]() ;
;
(方法二):如圖1,過點![]() 作
作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作直線
作直線![]() 與
與![]() 軸交于點
軸交于點![]() ,則
,則![]()
請你參照以上兩種方法,解決下列問題:
(1)已知點![]() ,點
,點![]() ,則
,則![]() 、
、![]() 兩點間的“2值”直角距離
兩點間的“2值”直角距離![]() .
.
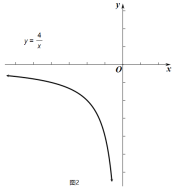
(2)函數![]() 的圖像如圖2所示,點
的圖像如圖2所示,點![]() 為其圖像上一動點,滿足
為其圖像上一動點,滿足![]() 兩點間的“
兩點間的“![]() 值”直角距離
值”直角距離![]() ,且符合條件的點
,且符合條件的點![]() 有且僅有一個,求出符合條件的“
有且僅有一個,求出符合條件的“![]() 值”和點
值”和點![]() 坐標.
坐標.
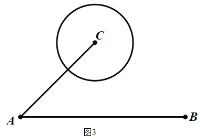
(3)城市的許多街道是相互垂直或平行的,因此,往往不能沿直線行走到達目的地,只能按直角拐彎的方式行走,因此,兩地之間修建垂直和平行的街道常常轉化為兩點間的“![]() 值”直角距離,
值”直角距離,![]() 地位于
地位于![]() 地的正東方向上,
地的正東方向上,![]() 地在
地在![]() 點東北方向上且相距
點東北方向上且相距![]() ,以
,以![]() 為圓心修建了一個半徑為
為圓心修建了一個半徑為![]() 的圓形濕地公園,現在要在公園和
的圓形濕地公園,現在要在公園和![]() 地之間修建觀光步道.步道只能東西或者南北走向,并且東西方向每千米成本是20萬元,南北方向每千米的成本是10萬元,問:修建這一規光步道至少要多少萬元?
地之間修建觀光步道.步道只能東西或者南北走向,并且東西方向每千米成本是20萬元,南北方向每千米的成本是10萬元,問:修建這一規光步道至少要多少萬元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC和△DEF均為等腰直角三角形,AB=2,DE=1,E、B、F、C在同一條直線上,開始時點B與點F重合,讓△DEF沿直線BC向右移動,最后點C與點E重合,設兩三角形重合面積為y,點F移動的距離為x,則y關于x的大致圖象是( )

A.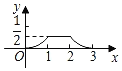 B.
B.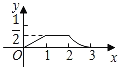
C.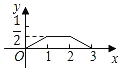 D.
D.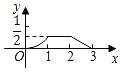
查看答案和解析>>
科目:初中數學 來源: 題型:
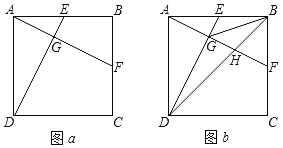
【題目】如圖a,在正方形ABCD中,E、F分別為邊AB、BC的中點,連接AF、DE交于點G.
(1)求證:AF⊥DE;
(2)如圖b,連接BG,BD,BD交AF于點H.
①求證:GB2=GAGD;
②若AB=10,求三角形GBH的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題呈現:
如圖 1,在邊長為 1 小的正方形網格中,連接格點 A、B 和 C、D,AB 和 CD 相交于點 P,求 tan ∠CPB 的值方法歸納:求一個銳角的三角函數值,我們往往需要找出(或構造出)一個直角三角形,觀察發現問題中∠ CPB不在直角三角形中,我們常常利用網格畫平行線等方法解決此類問題,比如連接格點 B、 E,可得 BE∥CD,則∠ABE=∠CPB,連接AE,那么∠CPB 就變換到 Rt△ABE 中.問題解決:
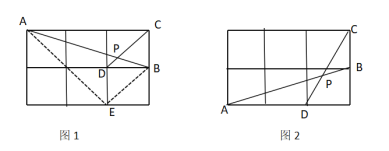
(1)直接寫出圖 1 中 tan CPB 的值為______;
(2)如圖 2,在邊長為 1 的正方形網格中,AB 與 CD 相交于點 P,求 cos CPB 的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
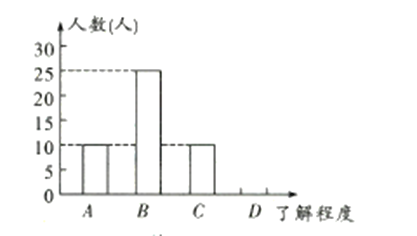
【題目】為響應市政府關于“垃圾不落地,市區更美麗”的主題宣傳活動,某校隨機調查了部分學生對垃圾分類知識的了解情況,對該校部分學生進行了問卷調查,并將調查結果分為![]() 四類(其中
四類(其中![]() 類表示“非常了解”,
類表示“非常了解”,![]() 類表示“比較了解”,
類表示“比較了解”,![]() 類表示“基本了解”,
類表示“基本了解”,![]() 類表示“不太了解”).根據調查結果得到如下不完整的統計表和統計圖.請解答下列問題:
類表示“不太了解”).根據調查結果得到如下不完整的統計表和統計圖.請解答下列問題:
了解程度 | 人數(人) | 所占百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,
,![]() .
.
![]() 補全條形統計圖;
補全條形統計圖;
![]() 若該校共有學生
若該校共有學生![]() 人,估計該校對垃圾分類知識“非常了解”的有多少人?
人,估計該校對垃圾分類知識“非常了解”的有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com