
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 從點
從點![]() 出發,沿對角線
出發,沿對角線![]() 向點
向點![]() 勻速運動,速度為
勻速運動,速度為![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,以
,以![]() 為一邊作正方形
為一邊作正方形![]() ,使得點
,使得點![]() 落在射線
落在射線![]() 上.點
上.點![]() 從點
從點![]() 出發,沿
出發,沿![]() 向點
向點![]() 勻速運動,速度為
勻速運動,速度為![]() ,以
,以![]() 為圓心,
為圓心,![]() 半徑作
半徑作![]() .點
.點![]() 與點
與點![]() 同時出發,設它們的運動時間為
同時出發,設它們的運動時間為![]() (單位:
(單位:![]() )
)![]() .
.
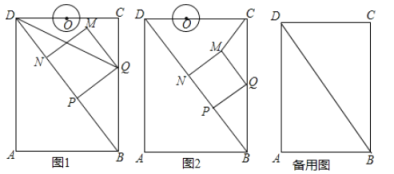
(1)如圖1,連接![]() ,若
,若![]() 平分
平分![]() ,則
,則![]() 的值為__________
的值為__________![]() ;
;
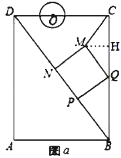
(2)如圖2,連接![]() ,設
,設![]() 的面積為
的面積為![]() ,求
,求![]() 關于t的函數關系式;
關于t的函數關系式;
(3)在運動過程中,當![]() 為何值時,
為何值時,![]() 與
與![]() 第一次相切?
第一次相切?
【答案】(1)1;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)首先根據題意得出DB的長,然后證明△BPQ~△BCD,據此利用相似三角形性質分析得出![]() 、
、![]() 、
、![]() ,最后利用角平分線性質進一步求解即可;
,最后利用角平分線性質進一步求解即可;
(2)過點![]() 作
作![]() 于點
于點![]() ,先證明△HMQ~△PQB,由此得出
,先證明△HMQ~△PQB,由此得出![]() ,最后根據三角形面積公式進一步計算即可;
,最后根據三角形面積公式進一步計算即可;
(3)設![]() 與
與![]() 相切于點
相切于點![]() ,連接
,連接![]() ,作
,作![]() 于點
于點![]() ,易得
,易得![]() ,然后進一步證明△DFO~△DCB,由此進一步求解即可.
,然后進一步證明△DFO~△DCB,由此進一步求解即可.
(1)∵四邊形![]() 為矩形,
為矩形,
∴![]() 、
、![]() ,∠A=∠C=90°,
,∠A=∠C=90°,
∴![]() ,
,
∵四邊形![]() 為正方形,
為正方形,
∴![]() 90°,
90°,
∵![]() ,
,
∴△BPQ~△BCD,
∴![]() ,即
,即![]() ,
,
則![]() 、
、![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
故答案為:1;
(2)如圖![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,
,
∴![]() 90°,
90°,
則![]() 90°,
90°,
∴![]() ,
,
∴△HMQ~△PQB,
∴![]() ,即
,即![]() ,則
,則![]() ,
,
∴![]() ;
;
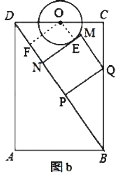
(3)如圖![]() ,設
,設![]() 與
與![]() 相切于點
相切于點![]() ,連接
,連接![]() ,作
,作![]() 于點
于點![]() ,
,
則四邊形![]() 為矩形,
為矩形,
∴![]() ,
,![]() 90°,
90°,
∵![]() ,
,
∴△DFO~△DCB,
∴![]() ,
,
即![]() ,
,
解得:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,經過正方形ABCD的頂點A在其外側作直線AP,點B關于直線AP的對稱點為E,連接BE、DE,其中DE交直線AP于點F.
(1)依題意補全圖1.
(2)若∠PAB=30°,求∠ADF的度數.
(3)如圖,若45°<∠PAB<90°,用等式表示線段AB,FE,FD之間的數量關系,并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
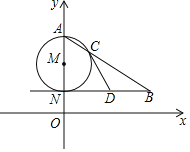
【題目】如圖,AN是⊙M的直徑,NB∥x軸,AB交⊙M于點C.
(1)若點A(0,6),N(0,2),∠ABN=30°,求點B的坐標;
(2)若D為線段NB的中點,求證:直線CD是⊙M的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
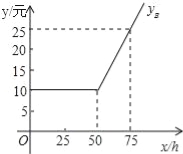
【題目】隨著信息技術的快速發展,“互聯網+”滲透到我們日常生活的各個領域,網上在線學習交流已不再是夢,現有某教學網站策劃了A,B兩種上網學習的月收費方式:
收費方式 | 月使用費/元 | 包時上網時間/h | 超時費/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
設每月上網學習時間為x小時,方案A,B的收費金額分別為yA,yB.
(1)如圖是yB與x之間函數關系的圖象,請根據圖象填空:m= ;n=
(2)寫出yA與x之間的函數關系式.
(3)選擇哪種方式上網學習合算,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年,中央全面落實“穩房價”的長效管控機制,重慶房市較上一年大幅降溫,11月,LH地產共推出了大平層和小三居兩種房型共80套,其中大平層每套面積180平方米,單價1.8萬元/平方米,小三居每套面積120平方米,單價1.5萬元/平方米.
(1)LH地產11月的銷售總額為18720萬元,問11月要推出多少套大平層房型?
(2)2019年12月,中央經濟會議上重申“房子是拿來住的,不是拿來炒的”,重慶房市成功穩定并略有回落.為年底清盤促銷,LH地產調整營銷方案,12月推出兩種房型的總數量仍為80套,并將大平層的單價在原有基礎上每平方米下調![]() 萬元(m>0),將小三居的單價在原有基礎上每平方米下調
萬元(m>0),將小三居的單價在原有基礎上每平方米下調![]() 萬元,這樣大平層的銷量較(1)中11月的銷量上漲了7m套,且推出的房屋全部售罄,結果12月的銷售總額恰好與(1)中I1月的銷售總額相等.求出m的值.
萬元,這樣大平層的銷量較(1)中11月的銷量上漲了7m套,且推出的房屋全部售罄,結果12月的銷售總額恰好與(1)中I1月的銷售總額相等.求出m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
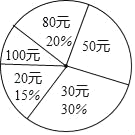
【題目】在“全民讀書月”活動中,小明調查了班級里40名同學本學期購買課外書的費用情況,并將結果繪制成如圖所示的統計表和扇形統計圖,請根據相關信息,解答下列問題:(直接填寫結果)
費用(元) | 20 | 30 | 50 | 80 | 100 |
人數 | 6 | a | 10 | b | 4 |
(1)本次調查獲取的樣本數據的眾數是 元,中位數是 元;
(2)扇形統計圖中,“50元”所對應的圓心角的度數為 度,該班學生購買課外書的平均費用為 元;
(3)若該校共有學生1000人,根據樣本數據,估計本學期購買課外書花費50元的學生有 人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級某班同學在“五四”游園活動中進行抽獎活動.在一個不透明的口袋中有三個完全相同的小球,把它們分別標號為A,B,C,隨機摸出一個小球記下標號后放回搖勻,再從中隨機摸出一個小球記下標號.
(1)請用列表或畫樹形圖的方法(只選其中一種),表示兩次摸出小球上的標號的所有結果;
(2)規定當兩次摸出的小球標號相同時中獎,求中獎的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,AB、CD相交于點O,△AOC≌△BOD,點E、F分別在OA、OB上,要使△EOC≌△FOD,添加的一個條件不可能是( )

A. ∠OCE=∠ODF B. ∠CEA=∠DFB C. CE=DF D. OE=OF
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com