
【題目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】試題分析:
根據兩方程的特點,使用“因式分解法”解兩方程即可.
試題解析:
(1)原方程可化為: ![]() ,
,
方程左邊分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化為: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【題型】解答題
【結束】
20
【題目】已知x1,x2是關于x的一元二次方程x2-2(m+1)x+m2+5=0的兩實根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一邊長為7,若x1,x2恰好是△ABC另外兩邊的邊長,求這個三角形的周長.
【答案】(1)m的值為6;(2)17.
【解析】試題分析:
(1)由題意和根與系數的關系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;從而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判別式”進行檢驗即可得到m的值;
(2)①當7為腰長時,則方程的兩根中有一根為7,代入方程可解得m的值(此時m的取值需滿足根的判別式△![]() ),將m的值代入原方程,可求得兩根(此時兩根和7需滿足三角形三邊之間的關系),從而可求得等腰三角形的周長;
),將m的值代入原方程,可求得兩根(此時兩根和7需滿足三角形三邊之間的關系),從而可求得等腰三角形的周長;
②當7為底邊時,則方程的兩根相等,由此可得“根的判別式△=0”,從而可得關于m的方程,解方程求得m的值,代入原方程可求得方程的兩根,再由三角形三邊之間的關系檢驗即可.
試題解析:
(1)(x1-1)(x2-1)=28,即x1x2-(x1+x2)=27,而x1+x2=2(m+1),x1x2=m2+5,
∴m2+5-2(m+1)=27,
解得m1=6,m2=-4,
又Δ=[-2(m+1)]2-4×1×(m2+5)≥0時,m≥2,
∴m的值為6;
(2) 若7為腰長,則方程x2-2(m+1)x+m2+5=0的一根為7,
即72-2×7×(m+1)+m2+5=0,
解得m1=10,m2=4,
當m=10時,方程x2-22x+105=0,根為x1=15,x2=7,不符合題意,舍去.
當m=4時,方程為x2-10x+21=0,根為x1=3,x2=7,此時周長為7+7+3=17
若7為底邊,則方程x2-2(m+1)x+m2+5=0有兩等根,
∴Δ=0,解得m=2,此時方程為x2-6x+9=0,根為x1=3,x2=3,3+3<7,不成立,
綜上所述,三角形周長為17


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D在BC上,DE∥AC,DF∥AB,下列四個判斷中不正確的是( )

A.四邊形AEDF是平行四邊形
B.若∠BAC=90°,則四邊形AEDF是矩形
C.若AD平分∠BAC,則四邊形AEDF是矩形
D.若AD⊥BC且AB=AC,則四邊形AEDF是菱形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,以A為圓心,任意長為半徑畫弧分別交AB,AC于點M和N,再分別以M、N為圓心,大于![]() MN的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列結論:①AD是∠BAC的平分線;②若∠B=30°,則DA=DB;③AB:AC=2:1;④點D在AB的垂直平分線上.一定成立的個數為( )
MN的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列結論:①AD是∠BAC的平分線;②若∠B=30°,則DA=DB;③AB:AC=2:1;④點D在AB的垂直平分線上.一定成立的個數為( )
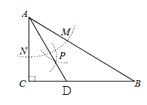
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F為BC中點,連接AE.
(1)直接寫出∠BAE的度數為 ;
(2)判斷AF與CE的位置關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是兩塊完全一樣的含30°角的直角三角尺,分別記做△ABC與△A′B′C′,現將兩塊三角尺重疊在一起,設較長直角邊的中點為M,繞中點M轉動上面的三角尺ABC,使其直角頂點C恰好落在三角尺A′B′C′的斜邊A′B′上.當∠A=30°,AC=10時,兩直角頂點C,C′間的距離是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】猜想與證明:小強想證明下面的問題:“有兩個角(圖中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心將圖弄臟了,只能看見圖中的
)相等的三角形是等腰三角形”.但他不小心將圖弄臟了,只能看見圖中的![]() 和邊
和邊![]() .
.
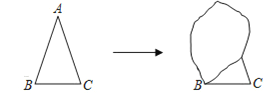
(1)請問:他能夠把圖恢復成原來的樣子嗎?若能,請你幫他寫出至少兩種以上恢復的方法并在備用圖上恢復原來的樣子.

(2)你能夠證明這樣的三角形是等腰三角形嗎?(至少用兩種方法證明)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若拋物線y=x2-2x+c與y軸的交點為(0,-3),則下列說法不正確的是( )
A.拋物線開口向上
B.拋物線的對稱軸是x=1
C.當x=1時,y的最大值為-4
D.拋物線與x軸的交點為(-1,0),(3,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下圖的轉盤被劃分成六個相同大小的扇形,并分別標上1,2,3,4,5,6這六個數字,指針停在每個扇形的可能性相等。四位同學各自發表了下述見解:
甲:如果指針前三次都停在了3號扇形,下次就一定不會停在3號扇形;
乙:只要指針連續轉六次,一定會有一次停在6號扇形;
丙:指針停在奇數號扇形的概率與停在偶數號扇形的概率相等;
丁:運氣好的時候,只要在轉動前默默想好讓指針停在6號扇形,指針停在6號扇形的可能性就會加大。
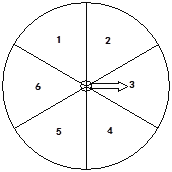
其中,你認為正確的見解有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com