
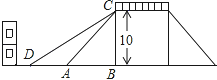
【題目】如圖是一座人行天橋的示意圖,天橋的高度是10米,CB⊥DB,坡面AC的傾斜角為45°.為了方便行人推車過天橋,市政部門決定降低坡度,使新坡面DC的坡度為i=![]() :3.若新坡角下需留3米寬的人行道,問離原坡角(A點處)10米的建筑物是否需要拆除?(參考數據:
:3.若新坡角下需留3米寬的人行道,問離原坡角(A點處)10米的建筑物是否需要拆除?(參考數據: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】隨著新農村的建設和舊城的改造,我們的家園越來越美麗,小明家附近廣場中央新修了一個圓形噴水池,在水池中心豎直安裝了一根高![]() 米的噴水管,它噴出的拋物線形水柱在與池中心的水平距離為米處達到最高,水柱落地處離池中心
米的噴水管,它噴出的拋物線形水柱在與池中心的水平距離為米處達到最高,水柱落地處離池中心![]() 米.
米.

(1)請你建立適當的直角坐標系,并求出水柱拋物線的函數解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內角∠ABC、外角∠ACF.以下結論:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正確的結論的有__________.(把正確結論的序號都寫上去)

查看答案和解析>>
科目:初中數學 來源: 題型:
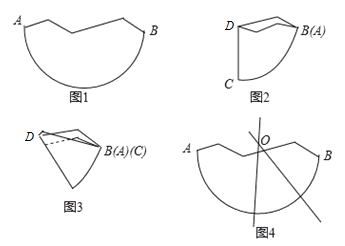
【題目】數學課上,老師介紹了利用尺規確定殘缺紙片圓心的方法.小華對數學老師說:“我可以用拆疊紙片的方法確定圓心”.小華的作法如下:
第一步:如圖1,將殘缺的紙片對折,使弧AB的端點A與端點B重合,得到圖2;
第二步:將圖2繼續對折,使弧CD的端點C與端點B重合,得到圖3;
第三步:將對折后的圖3打開如圖4,兩條折痕所在直線的交點即為圓心O.
老師肯定了他的作法.那么他確定圓心的依據是_____________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)6+(﹣![]() )﹣2﹣(﹣1.5)
)﹣2﹣(﹣1.5)
(2)10+[![]() ﹣(﹣1+1
﹣(﹣1+1![]() )]×6
)]×6
(3)﹣2÷![]() ×(
×(![]() )2
)2
(4)﹣32﹣|﹣6|﹣3×(﹣![]() )+(﹣2)2÷
)+(﹣2)2÷![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】求若干個相同的不為零的有理數的除法運算叫做除方.
如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 類比有理數的乘方,我們把 2÷2÷2 記作 2③,讀作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)記作(-3)④,讀作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)記作
(a≠0)記作![]() ,讀作“a的圈n次方”.
,讀作“a的圈n次方”.
(1)直接寫出計算結果: ![]() _____,
_____, ![]() _________,
_________, ![]() ___________,
___________,
(2)我們知道,有理數的減法運算可以轉化為加法運算,除法運算可以轉化為乘法運算,
請嘗試將有理數的除方運算轉化為乘方運算,歸納如下:一個非零有理數的圈 n 次方等于_____.
(3)計算 ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,A(a,b),B(c,0)是x軸正半軸上一點,∠ABO=30°,若![]() 與|2﹣a|互為相反數.
與|2﹣a|互為相反數.

(1)求c的值;
(2)如圖2,AC⊥AB交x軸于C,以AC為邊的正方形ACDE的對角線AD交x軸于F.
①求證:BE=2OC;
②記BF2﹣OF2=m,OC2=n,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數![]() (m為常數).
(m為常數).
(1)試判斷該函數的圖象與x軸的公共點的個數;
(2)求證:不論m為何值,該函數的圖象的頂點都在函數![]() 的圖象上;
的圖象上;
(3)若直線y=x與二次函數圖象交于A、B兩點,當﹣4≤m≤2時,求線段AB的最大值和最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com