
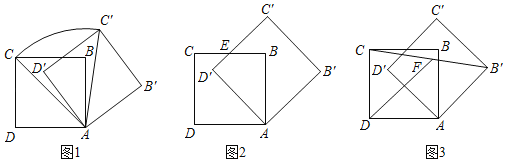
【題目】若邊長為6的正方形ABCD繞點A順時針旋轉,得正方形AB′C′D′,記旋轉角為a.
(I)如圖1,當a=60°時,求點C經過的弧![]() 的長度和線段AC掃過的扇形面積;
的長度和線段AC掃過的扇形面積;
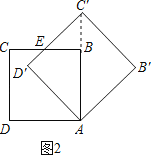
(Ⅱ)如圖2,當a=45°時,BC與D′C′的交點為E,求線段D′E的長度;
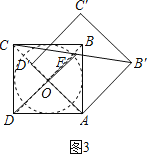
(Ⅲ)如圖3,在旋轉過程中,若F為線段CB′的中點,求線段DF長度的取值范圍.
【答案】(I)12π;(Ⅱ)D′E=6![]() ﹣6;(Ⅲ)3
﹣6;(Ⅲ)3![]() ﹣3≤DF≤3
﹣3≤DF≤3![]() +3.
+3.
【解析】
(Ⅰ)根據正方形的性質得到AD=CD=6,∠D=90°,由勾股定理得到AC=6![]() ,根據弧長的計算公式和扇形的面積公式即可得到結論;
,根據弧長的計算公式和扇形的面積公式即可得到結論;
(Ⅱ)連接BC′,根據題意得到B在對角線AC′上,根據勾股定理得到AC′=![]() =6
=6![]() ,求得BC′=6
,求得BC′=6![]() ﹣6,推出△BC′E是等腰直角三角形,得到C′E=
﹣6,推出△BC′E是等腰直角三角形,得到C′E=![]() BC′=12﹣6
BC′=12﹣6![]() ,于是得到結論;
,于是得到結論;
(Ⅲ)如圖3,連接DB,AC相交于點O,則O是DB的中點,根據三角形中位線定理得到FO=![]() AB′=3,推出F在以O為圓心,3為半徑的圓上運動,于是得到結論.
AB′=3,推出F在以O為圓心,3為半徑的圓上運動,于是得到結論.
解:(Ⅰ)∵四邊形ABCD是正方形,
∴AD=CD=6,∠D=90°,
∴AC=6![]() ,
,
∵邊長為6的正方形ABCD繞點A順時針旋轉,得正方形AB′C′D′,
∴∠CAC′=60°,
∴![]() 的長度=
的長度=![]() =2
=2![]() π,線段AC掃過的扇形面積=
π,線段AC掃過的扇形面積=![]() =12π;
=12π;
(Ⅱ)解:如圖2,連接BC′,
∵旋轉角∠BAB′=45°,∠BAD′=45°,
∴B在對角線AC′上,
∵B′C′=AB′=6,
在Rt△AB′C′中,AC′=![]() =6
=6![]() ,
,
∴BC′=6![]() ﹣6,
﹣6,
∵∠C′BE=180°﹣∠ABC=90°,∠BC′E=90°﹣45°=45°,
∴△BC′E是等腰直角三角形,
∴C′E=![]() BC′=12﹣6
BC′=12﹣6![]() ,
,
∴D′E=C′D′﹣EC′=6﹣(12﹣6![]() )=6
)=6![]() ﹣6;
﹣6;
(Ⅲ)如圖3,連接DB,AC相交于點O,
則O是DB的中點,
∵F為線段BC′的中點,
∴FO=![]() AB′=3,
AB′=3,
∴F在以O為圓心,3為半徑的圓上運動,
∵DO=3![]() ,
,
∴DF最大值為3![]() +3,DF的最小值為3
+3,DF的最小值為3![]() ﹣3,
﹣3,
∴DF長的取值范圍為3![]() ﹣3≤DF≤3
﹣3≤DF≤3![]() +3.
+3.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知線段![]() ,點
,點![]() 為線段外一點,且
為線段外一點,且![]() .
.
(1)請用直尺(不帶刻度)和圓規在線段![]() 上找一點
上找一點![]() ,使得
,使得![]() 的周長為
的周長為![]() (作圖不必寫作法,但要保留作圖痕跡);
(作圖不必寫作法,但要保留作圖痕跡);
(2)在(1)的條件下,若![]() ,
,![]() ,當
,當![]() 是等腰三角形時,求
是等腰三角形時,求![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為滿足社區居民健身的需要,區政府準備采購若干套健身器材免費提供給社區,經考察,康樂公司有甲,乙兩種型號的健身器材可供選擇.
(1)康樂公司2017年每套甲型健身器材的售價為2萬元,經過連續兩年降價,2019年每套售價為1.28萬元,求每套甲型健身器材售價的年平均下降率n;
(2)2019年市政府經過招標,決定年內采購并安裝康樂公司甲,乙兩種型號的健身器材共80套,采購專項經費總計不超過95萬元,采購合同規定:每套甲型健身器材售價為1.28萬元,每套乙型健身器材售價為1.4(1﹣n)萬元.
①甲型健身器材最多可購買多少套?
②按照甲型健身器材購買最多的情況下,安裝完成后,若每套甲型和乙型健身器材一年的養護費分別是購買價的8%和10%,區政府計劃支出9萬元進行養護,問該計劃支出能否滿足一年的養護需要?
查看答案和解析>>
科目:初中數學 來源: 題型:
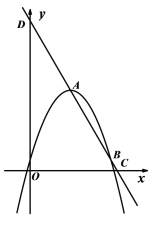
【題目】如圖所示,二次函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象交于A、B兩點,點B在點A的右側,直線AB分別交x軸、y軸于C、D兩點,且k<0.
的圖象交于A、B兩點,點B在點A的右側,直線AB分別交x軸、y軸于C、D兩點,且k<0.
(1)求A,B兩點橫坐標;
(2)若△OAB是以OA為腰的等腰三角形,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊AD⊥y軸,垂足為點E,頂點A在第二象限,頂點B在y軸的正半軸上,反比例函數y=![]() (k≠0,x>0)的圖象經過頂點C、D,若點C的橫坐標為5,BE=3DE,則k的值為______.
(k≠0,x>0)的圖象經過頂點C、D,若點C的橫坐標為5,BE=3DE,則k的值為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了創建文明城市,增弘環保意識,某班隨機抽取了8名學生(分別為A,B,C,D,E,F,G,H),進行垃圾分類投放檢測,檢測結果如下表,其中“√”表示投放正確,“×”表示投放錯誤,
學生 垃圾類別 | A | B | C | D | E | F | G | H |
可回收物 | √ | × | × | √ | √ | × | √ | √ |
其他垃圾 | × | √ | √ | √ | √ | × | √ | √ |
餐廚垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
有害垃圾 | × | √ | × | × | × | √ | × | √ |
(1)檢測結果中,有幾名學生正確投放了至少三類垃圾?請列舉出這幾名學生.
(2)為進一步了解學生垃圾分類的投放情況,從檢測結果是“有害垃圾”投放錯誤的學生中隨機抽取2名進行訪談,求抽到學生A的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
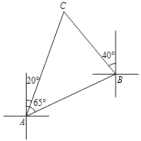
【題目】如圖,一艘船由![]() 港沿北偏東65°方向航行
港沿北偏東65°方向航行![]() 至
至![]() 港,然后再沿北偏西40°方向航行至
港,然后再沿北偏西40°方向航行至![]() 港,
港,![]() 港在
港在![]() 港北偏東20°方向,則
港北偏東20°方向,則![]() 兩港之間的距離為( )
兩港之間的距離為( )![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
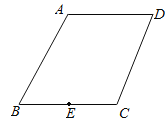
【題目】已知:如圖,四邊形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,點E為BC的中點,以CE為弦作圓,設該圓與四邊形ABCD的一邊的交點為P,若∠CPE=30°,則EP的長為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com