
【題目】如圖①,若二次函數y= ![]() x2+bx+c的圖象與x軸交于A(﹣2,0),B(3,0)兩點,點A關于正比例函數y=
x2+bx+c的圖象與x軸交于A(﹣2,0),B(3,0)兩點,點A關于正比例函數y= ![]() x的圖象的對稱點為C.
x的圖象的對稱點為C.
(1)求b、c的值;
(2)證明:點C在所求的二次函數的圖象上;
(3)如圖②,過點B作DB⊥x軸交正比例函數y= ![]() x的圖象于點D,連結AC,交正比例函數y=
x的圖象于點D,連結AC,交正比例函數y= ![]() x的圖象于點E,連結AD、CD.如果動點P從點A沿線段AD方向以每秒2個單位的速度向點D運動,同時動點Q從點D沿線段DC方向以每秒1個單位的速度向點C運動.當其中一個點到達終點時,另一個點隨之停止運動,連結PQ、QE、PE.設運動時間為t秒,是否存在某一時刻,使PE平分∠APQ,同時QE平分∠PQC?若存在,求出t的值;若不存在,請說明理由.
x的圖象于點E,連結AD、CD.如果動點P從點A沿線段AD方向以每秒2個單位的速度向點D運動,同時動點Q從點D沿線段DC方向以每秒1個單位的速度向點C運動.當其中一個點到達終點時,另一個點隨之停止運動,連結PQ、QE、PE.設運動時間為t秒,是否存在某一時刻,使PE平分∠APQ,同時QE平分∠PQC?若存在,求出t的值;若不存在,請說明理由.
【答案】
(1)
解:∵點A(﹣2,0),B(3,0)在拋物線y= ![]() x2+bx+c上,
x2+bx+c上,
∴ 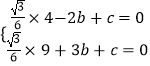 ,
,
解得:b=﹣ ![]() ,c=﹣
,c=﹣ ![]()
(2)
解:設點F在直線y= ![]() x上,且F(2,
x上,且F(2, ![]() ).
).
如答圖1所示,過點F作FH⊥x軸于點H,則FH= ![]() ,OH=2,
,OH=2,
∴tan∠FOB= ![]() =
= ![]() ,∴∠FOB=60°.
,∴∠FOB=60°.
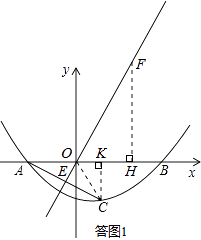
∴∠AOE=∠FOB=60°.
連接OC,過點C作CK⊥x軸于點K.
∵點A、C關于y= ![]() x對稱,∴OC=OA=2,∠COE=∠AOE=60°.
x對稱,∴OC=OA=2,∠COE=∠AOE=60°.
∴∠COK=180°﹣∠AOE﹣∠COE=60°.
在Rt△COK中,CK=OCsin60°=2× ![]() =
= ![]() ,OK=OCcos60°=2×
,OK=OCcos60°=2× ![]() =1.
=1.
∴C(1,﹣ ![]() ).
).
拋物線的解析式為:y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,當x=1時,y=﹣
,當x=1時,y=﹣ ![]() ,
,
∴點C在所求二次函數的圖象上
(3)
解:假設存在.
如答圖1所示,在Rt△ACK中,由勾股定理得:AC= ![]() =
= ![]() =
= ![]() .
.
如答圖2所示,∵OB=3,∴BD=3 ![]() ,AB=OA+OB=5.
,AB=OA+OB=5.
在Rt△ABD中,由勾股定理得:AD= ![]() =
= ![]() =2
=2 ![]() .
.
∵點A、C關于y= ![]() x對稱,
x對稱,
∴CD=AD=2 ![]() ,∠DAC=∠DCA,AE=CE=
,∠DAC=∠DCA,AE=CE= ![]() AC=
AC= ![]() .
.
連接PQ、PE,QE,則∠APE=∠QPE,∠PQE=∠CQE.
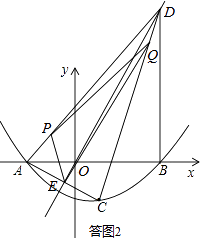
在四邊形APQC中,∠DAC+∠APQ+∠PQC+∠DCA=360°(四邊形內角和等于360°),
即2∠DAC+2∠APE+2∠CQE=360°,
∴∠DAC+∠APE+∠CQE=180°.
又∵∠DAC+∠APE+∠AEP=180°(三角形內角和定理),
∴∠AEP=∠CQE.
在△APE與△CEQ中,∵∠DAC=∠DCA,∠AEP=∠CQE,
∴△APE∽△CEQ,
∴ ![]() ,即:
,即: ![]() ,
,
整理得:2t2﹣ ![]() t+3=0,
t+3=0,
解得:t= ![]() 或t=
或t= ![]() (t<
(t< ![]() ,所以舍去)
,所以舍去)
∴存在某一時刻,使PE平分∠APQ,同時QE平分∠PQC,此時t= ![]()
【解析】(1)利用待定系數法求出b,c的值;(2)如答圖1所示,關鍵是求出點C的坐標.首先求出直線y= ![]() x與x軸所夾銳角為60°,則可推出在Rt△COK中,∠COK=60°,解此直角三角形即可求出點C的坐標;(3)如答圖2所示,關鍵是證明△APE∽△CEQ.根據∠DAC=∠DCA,∠AEP=∠CQE,證明△APE∽△CEQ,根據相似線段比例關系列出方程,解方程求出時間t的值.
x與x軸所夾銳角為60°,則可推出在Rt△COK中,∠COK=60°,解此直角三角形即可求出點C的坐標;(3)如答圖2所示,關鍵是證明△APE∽△CEQ.根據∠DAC=∠DCA,∠AEP=∠CQE,證明△APE∽△CEQ,根據相似線段比例關系列出方程,解方程求出時間t的值.
【考點精析】本題主要考查了二次函數的圖象和二次函數的性質的相關知識點,需要掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AB∥CD,AD∥BC, AB=3,BC=4,將矩形紙片沿BD折疊,使點A落在點E處,設DE與BC相交于點F.
(1)判斷△BDF的形狀,并說明理由;
(2)求DF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【閱讀】
如圖1,在平面直角坐標系xOy中,已知點A(a,0)(a>0),B(2,3),C(0,3).過原點O作直線l,使它經過第一、三象限,直線l與y軸的正半軸所成角設為θ,將四邊形OABC的直角∠OCB沿直線l折疊,點C落在點D處,我們把這個操作過程記為FZ[θ,a].
(1)【理解】
若點D與點A重合,則這個操作過程為FZ[ , ];
(2)【嘗試】
若點D恰為AB的中點(如圖2),求θ;
(3)經過FZ[45°,a]操作,點B落在點E處,若點E在四邊形0ABC的邊AB上,求出a的值;若點E落在四邊形0ABC的外部,直接寫出a的取值范圍;
(4)【探究】
經過FZ[θ,a]操作后,作直線CD交x軸于點G,交直線AB于點H,使得△ODG與△GAH是一對相似的等腰三角形,直接寫出FZ[θ,a].
查看答案和解析>>
科目:初中數學 來源: 題型:
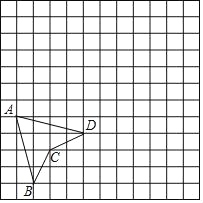
【題目】如圖,方格紙中每個小正方形的邊長為1,四邊形ABCD的頂點都在格點上.
(1)在方格紙上建立平面直角坐標系,使四邊形ABCD的頂點A,C的坐標分別為(﹣5,﹣1),(﹣3,﹣3),并寫出點D的坐標;
(2)在(1)中所建坐標系中,畫出四邊形ABCD關于x軸的對稱圖形A1B1C1D1,并寫出點B的對應點B1的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,E為BC邊上的一點,連結AE、BD且AE=AB. 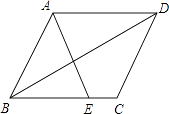
(1)求證:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求證:四邊形ABCD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2012年我國國民經濟運行總體平穩,全年全國公共財政收入117210億元,2008﹣2012年全國公共財政收入及其增長速度情況如圖所示: 
(1)這五年中全國公共財政收入增長速度最高的年份是年;
(2)2012年的全國公共財政收入比2011年多億元;
(3)這五年的全國公共財政收入增長速度的平均數是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y= ![]() x2+bx﹣
x2+bx﹣ ![]() 的圖象與x軸交于點A(﹣3,0)和點B,以AB為邊在x軸上方作正方形ABCD,點P是x軸上一動點,連接DP,過點P作DP的垂線與y軸交于點E.
的圖象與x軸交于點A(﹣3,0)和點B,以AB為邊在x軸上方作正方形ABCD,點P是x軸上一動點,連接DP,過點P作DP的垂線與y軸交于點E.
(1)請直接寫出點D的坐標:;
(2)當點P在線段AO(點P不與A、O重合)上運動至何處時,線段OE的長有最大值,求出這個最大值;
(3)是否存在這樣的點P,使△PED是等腰三角形?若存在,請求出點P的坐標及此時△PED與正方形ABCD重疊部分的面積;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD⊥BC于D , 下列條件:①∠B+∠DAC=90°;②∠B=∠DAC;③ ![]() =
= ![]() ;④AB2=BDBC . 其中一定能夠判定△ABC是直角三角形的有( )
;④AB2=BDBC . 其中一定能夠判定△ABC是直角三角形的有( ) 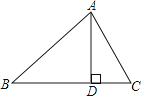
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com