
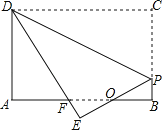
【題目】如圖,矩形紙片ABCD,AB=4,BC=3,點P在BC邊上,將△CDP沿DP折疊,點C落在點E處,PE、DE分別交AB于點O、F,且OP=OF,則cos∠ADF的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】根據折疊的性質可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP(AAS),根據全等三角形的性質可得出OE=OB、EF=BP,設EF=x,則BP=x、DF=4﹣x、BF=PC=3﹣x,進而可得出AF=1+x,在Rt△DAF中,利用勾股定理可求出x的值,再利用余弦的定義即可求出cos∠ADF的值.
根據折疊,可知:△DCP≌△DEP,
∴DC=DE=4,CP=EP.
在△OEF和△OBP中,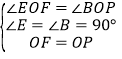 ,
,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP.
設EF=x,則BP=x,DF=DE﹣EF=4﹣x,
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC﹣BP=3﹣x,
∴AF=AB﹣BF=1+x.
在Rt△DAF中,AF2+AD2=DF2,即(1+x)2+32=(4﹣x)2,
解得:x=![]() ,
,
∴DF=4﹣x=![]() ,
,
∴cos∠ADF=![]() ,
,
故選C.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:初中數學 來源: 題型:
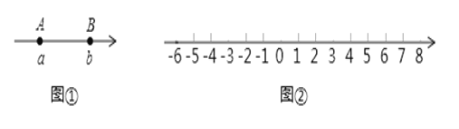
【題目】數軸上線段的長度可以用線段端點表示的數進行減法運算得到,例如:如圖①,若點![]() 在數軸上分別對應的數為
在數軸上分別對應的數為![]() ,則
,則![]() 的長度可以表示為
的長度可以表示為![]() .
.
請你用以上知識解決問題:
如圖②,一個點從數軸上的原點開始,先向左移動![]() 個單位長度到達
個單位長度到達![]() 點,再向右移動
點,再向右移動![]() 個單位長度到達
個單位長度到達![]() 點,然后向右移動
點,然后向右移動![]() 個單位長度到達
個單位長度到達![]() 點.
點.
![]() 請你在圖②的數軸上表示出
請你在圖②的數軸上表示出![]() 三點的位置.
三點的位置.
![]() 若點
若點![]() 以每秒
以每秒![]() 個單位長度的速度向左移動,同時,點
個單位長度的速度向左移動,同時,點![]() 和點
和點![]() 分別以每秒
分別以每秒![]() 個單位長度和
個單位長度和![]() 個單位長度的速度向右移動,設移動時間為
個單位長度的速度向右移動,設移動時間為![]() 秒.
秒.
①當![]() 時,求
時,求![]() 和
和![]() 的長度;
的長度;
②試探究:在移動過程中,![]() 的值是否隨著時間
的值是否隨著時間![]() 的變化而改變?若變化,請說明理由;若不變,請求其值.
的變化而改變?若變化,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 以下沿AB折疊的方法中,不一定能判定紙帶兩條邊a,b互相平行的是( )
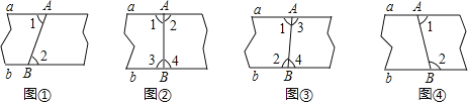
A.如圖①,展開后測得∠1=∠2B.如圖②,展開后測得∠1=∠2,且∠3=∠4
C.如圖③,展開后測得∠1=∠2,且∠3=∠4D.如圖④,展開后測得∠1+∠2=180°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠CAB=∠DBA,再添加一個條件,不一定能判定△ABC≌△BAD的是( )
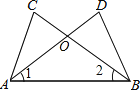
A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E是AD上一點,F是BA延長線上的一點,AF=AE,.
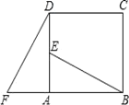
(1)求證:△ABE≌△ADF
(2)線段BE與DF有什么關系?證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點O是等邊三角形ABC內一點,∠AOB=110°,∠BOC=α, 以OC為邊作等邊三角形OCD,連接AD.

(1)當α=150°時,試判斷△AOD的形狀,并說明理由;
(2)探究:當a為多少度時,△AOD是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的周長為19,點D,E在邊BC上,∠ABC的平分線垂直于AE,垂足為N,∠ACB的平分線垂直于AD,垂足為M,若BC=7,則MN的長度為( )
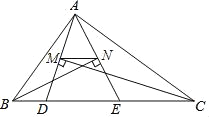
A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,以斜邊AB為邊向外作正方形ABDE,且正方形對角線交于點O,連接OC,已知AC=![]() ,OC=
,OC=![]() ,則另一直角邊BC的長為__________.
,則另一直角邊BC的長為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠A=∠C=90°,BE,DF分別是∠ABC,∠ADC的平分線.

(1)∠1與∠2有什么關系,為什么?
(2)BE與DF有什么關系?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com