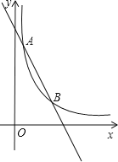
【題目】如圖，已知反比例函數
的圖象與一次函數y=kx+b的圖象交于點A（1，m），B （n，2）兩點
（1）求一次函數的解析式;
（2）直接寫出不等式
≥kx+b的解集；
長江作業本同步練習冊系列答案科目：初中數學 來源： 題型：
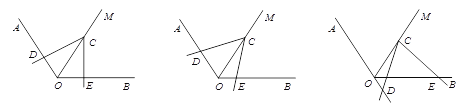
【題目】如圖，已知∠AOB=120°，在∠AOB的平分線OM上有一點C，將一個60°角的頂點與點C重合，它的兩條邊分別與直線OA、OB相交于點D、E．
（1）當∠DCE繞點C旋轉到CD與OA垂直時（如圖1），請猜想OE+OD與OC的數量關系，并說明理由；
（2）當∠DCE繞點C旋轉到CD與OA不垂直時，到達圖2的位置，（1）中的結論是否成立？并說明理由；
（3）當∠DCE繞點C旋轉到CD與OA的反向延長線相交時，上述結論是否成立？若成立，請給于證明；若不成立，線段OD、OE與OC之間又有怎樣的數量關系？請寫出你的猜想，不需證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解某中學學生對“厲行勤儉節約，反對鋪張浪費”主題活動的參與情況，小強在全校范圍內隨機抽取了若干名學生并就某日午飯浪費飯菜情況進行了調查，將調查內容分為四組：
飯和菜全部吃完；
：有剩飯但菜吃完；
：飯吃完但菜有剩；
：飯和菜都有剩.根據調查結果，繪制了如圖所示兩幅不完整的統計圖.
回答下列問題：
（1）這次被抽查的學生共有 人，扇形統計圖中，“組”所對應的圓心角的度數為 ；
（2）補全條形統計圖；
（3）已知該中學共有學生
人，請估計這日午飯有剩飯的學生人數，若按平均每人剩
克米飯計算，這日午飯將浪費多少千克米飯？
查看答案和解析>>
科目：初中數學 來源： 題型：
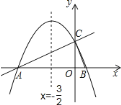
【題目】如圖，在平面直角坐標系中，直線
與
軸交于點
，與
軸交于點
，拋物線
的對稱軸是
且經過、兩點，與軸的另一交點為點
，連結
．
（1）填空：點、點和點的坐標分別為________，________，________；
（2）求證：
；
（3）求拋物線解析式；
（4）若點
為直線
上方的拋物線上的一點，連結
，
，求
面積的最大值，并求出此時點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，是根據九年級某班50名同學一周的鍛煉情況繪制的條形統計圖，下面關于該班50名同學一周鍛煉時間的說法錯誤的是（ ）
A.平均數是6
B.中位數是6.5
C.眾數是7
D.平均每周鍛煉超過6小時的人數占該班人數的一半
查看答案和解析>>
科目：初中數學 來源： 題型：
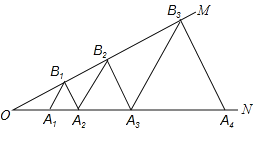
【題目】如圖，∠MON＝30°，點A1、A2、A3、……在射線ON上，點B1、B2、B3、……在射線OM上，△A1B1A2、△A2B2A3、△A3B3A4，……均為等邊三角形，若OA1＝1，則△A2019B2019A2020的邊長為__________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，⊙C的半徑為r，P是與圓心C不重合的點，點P關于⊙C的反稱點的定義如下：若在射線CP上存在一點P′，滿足CP+CP′=2r，則稱P′為點P關于⊙C的反稱點，如圖為點P及其關于⊙C的反稱點P′的示意圖．
特別地，當點P′與圓心C重合時，規定CP′=0．
（1）當⊙O的半徑為1時．
①分別判斷點M（2，1），N（
，0），T（1， 
）關于⊙O的反稱點是否存在？若存在，求其坐標；
②點P在直線y=﹣x+2上，若點P關于⊙O的反稱點P′存在，且點P′不在x軸上，求點P的橫坐標的取值范圍；
（2）⊙C的圓心在x軸上，半徑為1，直線y=﹣
x+2
與x軸、y軸分別交于點A，B，若線段AB上存在點P，使得點P關于⊙C的反稱點P′在⊙C的內部，求圓心C的橫坐標的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】近年來，共享單車逐漸成為高校學生喜愛的“綠色出行”方式之一，自2016年國慶后，許多高校均投放了使用手機支付就可隨取隨用的共享單車．某高校為了解本校學生出行使用共享單車的情況，隨機調查了某天部分出行學生使用共享單車的情況，并整理成如下統計表．
使用次數 | 0 | 1 | 2 | 3 | 4 | 5 |
人數 | 11 | 15 | 23 | 28 | 18 | 5 |
（1）這天部分出行學生使用共享單車次數的中位數是 ，眾數是 ，該中位數的意義是 ；
（2）這天部分出行學生平均每人使用共享單車約多少次？（結果保留整數）
（3）若該校某天有1500名學生出行，請你估計這天使用共享單車次數在3次以上（含3次）的學生有多少人？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
