
【題目】已知a、b、c為三角形的三邊,求證:方程a2x2![]() (a2+c2
(a2+c2![]() b2)x+c2=0沒有實數根.
b2)x+c2=0沒有實數根.
【答案】詳見解析.
【解析】
將根的判別式△=(a2+c2![]() b2)2
b2)2![]() 4a2c2運用平方差公式和完全平方公式進行變形,再根據三角形任意兩邊之和大于第三邊,兩邊之差小于第三邊,可以得到△<0.
4a2c2運用平方差公式和完全平方公式進行變形,再根據三角形任意兩邊之和大于第三邊,兩邊之差小于第三邊,可以得到△<0.
解:∵a,b,c為△ABC的三邊長,
∴a2≠0.
∴△=(a2+c2![]() b2)2
b2)2![]() 4a2c2
4a2c2
=(a2+c2![]() b2+2ac)(a2+c2
b2+2ac)(a2+c2![]() b2
b2![]() 2ac)
2ac)
=[(a+c)2![]() b2][(a
b2][(a![]() c)2
c)2![]() b2],
b2],
=(a+b+c)(a+c![]() b)(a
b)(a![]() c+b)(a
c+b)(a![]() c
c![]() b),
b),
又∵三角形任意兩邊之和大于第三邊,兩邊之差小于第三邊
∴a+b+c >0, a+c![]() b >0, a
b >0, a![]() c+b >0, a
c+b >0, a![]() c
c![]() b <0,
b <0,
∴(a+b+c)(a+c![]() b)(a
b)(a![]() c+b)(a
c+b)(a![]() c
c![]() b)<0
b)<0
∴△<0,∴原方程沒有實數根.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中數學 來源: 題型:
【題目】某數學興趣小組研究我國古代《算法統宗》里這樣一首詩:我問開店李三公,眾客都來到店中,一房七客多七客,一房九客一房空.詩中后兩句的意思是:如果每一間客房住7人,那么有7人無房可住;如果每一間客房住9人,那么就空出一間房.
(1)求該店有客房多少間?房客多少人?
(2)假設店主李三公將客房進行改造后,房間數大大增加.每間客房收費20錢,且每間客房最多入住4人,一次性定客房18間以上(含18間),房費按8折優惠.若詩中“眾客”再次一起入住,他們如何訂房更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋里裝有分別標有數字1,2,3,4四個小球,除數字不同外,小球沒有任何區別,每次實驗先攪拌均勻.
(1)若從中任取一球,球上的數字為偶數的概率為多少?
(2)若從中任取一球(不放回),再從中任取一球,請用畫樹狀圖或列表格的方法求出兩個球上的數字之和為偶數的概率.
(3)若設計一種游戲方案:從中任取兩球,兩個球上的數字之差的絕對值為1為甲勝,否則為乙勝,請問這種游戲方案設計對甲、乙雙方公平嗎?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A城氣象臺測得臺風中心在A城正西方向600km的B處,以每小時200km的速度向北偏東60°的方向移動,距臺風中心500km的范圍內是受臺風影響的區域.

(1)A城是否受到這次臺風的影響?為什么?
(2)若A城受到這次臺風的影響,那么A城遭受這次臺風影響有多長時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場用14500元購進甲、乙兩種礦泉水共500箱,礦泉水的成本價與銷售價如表(二)所示:
類別 | 成本價(元/箱) | 銷售價(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)購進甲、乙兩種礦泉水各多少箱?
(2)該商場售完這500箱礦泉水,可獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC=5,cos∠ABC=0.6,將△ABC繞點C順時針旋轉,得到△A1B1C.
(1)如圖1,當點B1在線段BA延長線上時.①求證:BB1∥CA1;②求△AB1C的面積;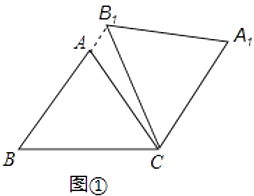
(2)如圖2,點E是BC邊的中點,點F為線段AB上的動點,在△ABC繞點C順時針旋轉過程中,點F的對應點是F1 , 求線段EF1長度的最大值與最小值的差.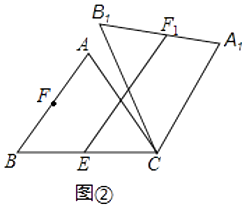
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“龜兔賽跑”的故事同學們都聽過,圖中的線段OD和折線OABC表示龜兔賽跑時路程與時間的關系,請根據圖中的信息,解決下列問題:
(1)填空:折線OABC表示賽跑過程中_________(填“兔子”或“烏龜”)的路程與時間的關系,賽跑的全程是_______米.
(2)兔子在起初每分鐘跑多少米?烏龜每分鐘爬多少米?
(3)烏龜用了多少分鐘追上了正在睡覺的兔子?
(4)兔子醒來后以400米/分鐘的速度跑向終點,結果還是比烏龜晚到了0.5分鐘,請你算算兔子中間停下睡覺用了多少時間?
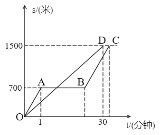
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形網格中,小格的頂點叫做格點。小華按下列要求作圖:①在正方形網格的三條不同的實線上各取一個格點,使其中任意兩點不在同一條實線上;②連結三個格點,使之構成直角三角形。小華在左邊的正方形網格中作出了Rt⊿ABC。請你按照同樣的要求,在右邊的兩個正方形網格中各畫出一個直角三角形,并使三個網格中的直角三角形互不全等。



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】蕪湖長江大橋是中國跨度最大的公路和鐵路兩用橋梁,大橋采用低塔斜拉橋橋型(如甲圖),圖乙是從圖甲引申出的平面圖,假設你站在橋上測得拉索AB與水平橋面的夾角是30°,拉索CD與水平橋面的夾角是60°,兩拉索頂端的距離BC為2米,兩拉索底端距離AD為20米,請求出立柱BH的長.(結果精確到0.1米, ![]() ≈1.732)
≈1.732)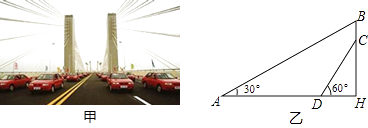
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com