
【題目】問題探究:三角形的角平分線是初中幾何中一條非常重要的線段,它除了具有平分角、角平分線上的點到角兩邊的距離相等這些性質外,還具有以下的性質:
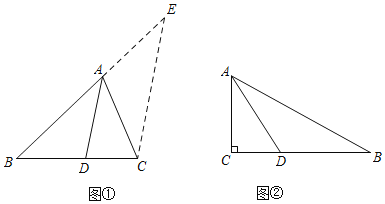
如圖①,在△ABC中,AD平分∠BAC交BC于點D,則![]() =
=![]() .提示:過點C作CE∥AD交BA的延長線于點E.
.提示:過點C作CE∥AD交BA的延長線于點E.
請根據上面的提示,寫出得到“![]() ”這一結論完整的證明過程.
”這一結論完整的證明過程.
結論應用:如圖②,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于點D.請直接利用“問題探究”的結論,求線段CD的長.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知平行四邊形ABCD,過點A作BC的垂線,垂足為點E,且滿足AE=EC,過點C作AB的垂線,垂足為點F,交AE于點G,連接BG.

(1)如圖1,若AC=![]() ,CD=4,求BC的長度;
,CD=4,求BC的長度;
(2)如圖2取AC上一點Q,連接EQ,在△QEC內取一點,連接QH,EH,過點H作AC的垂線,垂足為點P,若QH=EH,∠QEH=45°.求證:AQ=2HP.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y1:y=2(x﹣3)2+1和拋物線y2:y=﹣2x2﹣8x﹣3,若無論k取何值,直線y=kx+km+n被兩條拋物線所截的兩條線段都保持相等,則m=_____,n=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某大學生創業團隊有研發、管理和操作三個小組,各組的日工資和人數如下表所示.現從管理組分別抽調1人到研發組和操作組,調整后與調整前相比,下列說法中不正確的是( )
操作組 | 管理組 | 研發組 | |
日工資(元/人) | 260 | 280 | 300 |
人數(人) | 4 | 4 | 4 |
A.團隊平均日工資不變B.團隊日工資的方差不變
C.團隊日工資的中位數不變D.團隊日工資的極差不變
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點H,點F是![]() 上一點,連接AF交CD的延長線于點E.
上一點,連接AF交CD的延長線于點E.
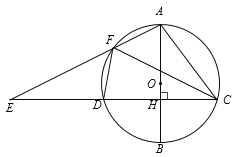
(1)求證:△AFC∽△ACE;
(2)若AC=5,DC=6,當點F為![]() 的中點時,求AF的值.
的中點時,求AF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解 在研究函數![]() 的圖象性質時,我們用“描點”的方法畫出函數的圖象.
的圖象性質時,我們用“描點”的方法畫出函數的圖象.
列出表示幾組![]() 與
與![]() 的對應值:
的對應值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描點連線:以表中各對對應值為坐標,描出各點,并用平滑的曲線順次連接這些點,就得到函數![]() 的圖象,如圖1:
的圖象,如圖1:
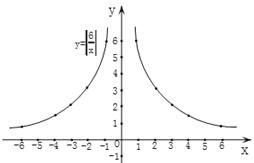
圖1
可以看出,這個函數圖象的兩個分支分別在第一、二象限,且當![]() 時,與函數
時,與函數![]() 在第一象限的圖象相同;當
在第一象限的圖象相同;當![]() 時,與函數
時,與函數![]() 在第二象限的圖象相同.類似地,我們把函數
在第二象限的圖象相同.類似地,我們把函數![]() (
(![]() 是常數,
是常數,![]() )的圖象稱為“并進雙曲線”.
)的圖象稱為“并進雙曲線”.
認真觀察圖表,分別寫出“并進雙曲線”![]() 的對稱性、函數的增減性性質:
的對稱性、函數的增減性性質:
①圖象的對稱性性質: ;
②函數的增減性性質: ;
延伸探究如圖2,點M,N分別在“并進雙曲線”![]() 的兩個分支上,
的兩個分支上,![]() ,判斷
,判斷![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
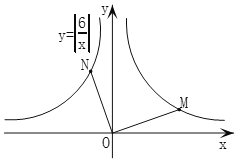
圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
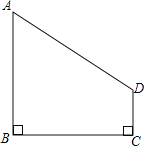
【題目】在四邊形ABCD中,∠B=∠C=90°,若AB=4,BC=4,CD=1,問:在BC上是否存在點P,使得AP⊥PD?若存在,求出BP的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有三張形狀大小完全相同的牌,正面分別標有數字2,3,5.將三張牌背面朝上,洗勻后放在桌子上.
(1)從中任取一張,求取到偶數的概率.
(2)甲、乙兩人進行摸牌游戲.
①甲從中隨機抽取一張牌,記錄數字后放回洗勻,乙再隨機抽取一張.請用列表法或畫樹狀圖的方法,求兩人抽取相同數字的概率;
②若兩人抽取的數字和為2的倍數,則甲獲勝;若抽取的數字和為5的倍數,則乙獲勝.這個游戲公平嗎?請用概率的知識加以解釋.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】桌面倒扣著背面圖案相同的四張卡片,其正面分別標記有數字![]() ,先任意抽取一張,卡片上的數記作x,不放回,再抽取一張,卡片上的數字記作y,設點A的坐標為(x,y).
,先任意抽取一張,卡片上的數記作x,不放回,再抽取一張,卡片上的數字記作y,設點A的坐標為(x,y).
(1)用樹狀圖或列表法列舉點A所有的坐標情況;
(2)求點A在拋物線![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com