【題目】如圖所示，A、B兩地相距50千米，甲于某日下午1時騎自行車從A地出發駛往B地，乙也于同日下午騎摩托車按相同路線從A地出發駛往B地，如圖所示，圖中的折線PQR和線段MN分別表示甲、乙所行駛的路程S和時間t的關系.象回答下列問題：
(1)甲和乙哪一個出發的更早?早出發多長時間?
(2)甲和乙哪一個早到達B城?早多長時間?
(3)乙騎摩托車的速度和甲騎自行車在全程的平均速度分別是多少?
(4)請你根據圖象上的數據，求出乙出發后多長時間追上甲?
【答案】（1）甲更早,早出發1 h;（2）乙更早,早到2 h;（3）甲的平均速度12.5km/h, 乙的平均速度是50km/h;(4) 乙出發0.5 h就追上甲
【解析】
（1）（2）讀圖可知；
（3）從圖中得：甲和乙所走的路程都是50千米，甲一共用了4小時，乙一共用了1小時，根據速度=
，代入計算得出；
（4）從圖中得：甲在走完全程時，前1小時速度為20千米/小時，從第2小時開始，速度為
=10千米/小時，因此設乙出發x小時就追上甲，則從圖中看，是在甲速度為10千米/小時時與乙相遇，所以甲的路程為20+10x，乙的路程為50x，列方程解出即可．
（1）甲下午1時出發，乙下午2時出發，所以甲更早，早出發1小時；
（2）甲5時到達，乙3時到達，所以乙更早，早到2小時；
（3）乙的速度=
=50（千米/時），甲的平均速度=
=12.5（千米/時）；
（4）設乙出發x小時就追上甲，根據題意得：50x=20+10x，x=0.5．
答：乙出發0.5小時就追上甲．
科目：初中數學 來源： 題型：
【題目】圖①為一種平板電腦保護套的支架效果圖，AM固定于平板電腦背面，與可活動的MB、CB部分組成支架．平板電腦的下端N保持在保護套CB上．不考慮拐角處的弧度及平板電腦和保護套的厚度，繪制成圖②．其中AN表示平板電腦，M為AN上的定點，AN＝CB＝20 cm，AM＝8 cm，MB＝MN．我們把∠ANB叫做傾斜角．
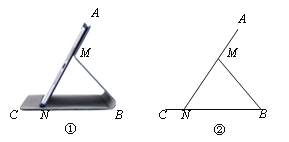
（1）當傾斜角為45°時，求CN的長；
（2）按設計要求，傾斜角能小于30°嗎？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我圍古代數學的許多創新和發展都位居世界前列，如南宋數學家楊輝(約13世紀)所著的《詳解九章算術》一書中，用如圖的三角形解釋二項和(a+b)“的展開式的各項系數，此三角形稱為“楊輝三角”.
根據“楊輝三角”請計算(a+b)20的展開式中第三項的系數為________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在平面直角坐標系xOy中，A（0，4），B（8，0），C（8，4）．
（1）試說明四邊形AOBC是矩形．
（2）在x軸上取一點D，將△DCB繞點C順時針旋轉90°得到
（點
與點D對應）．若OD＝3，求點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，已知∠CDB＝110°，∠ABD＝30°．
（1）請用直尺和圓規在圖中直接作出∠A的平分線AE交BD于E；（不寫作法，保留作圖痕跡）
（2）在（1）的條件下，求出∠AED的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】.如圖，點A、B、D、E在⊙O上，弦AE、BD的延長線相交于點C．若AB是⊙O的直徑，D是BC的中點．
（1）試判斷AB、AC之間的大小關系，并給出證明；
（2）在上述題設條件下，當△ABC為正三角形時，點E是否AC的中點？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
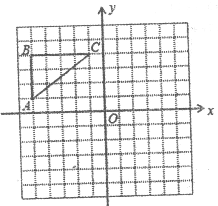
【題目】如圖，在正方形網絡中，△ABC各頂點都在格點上，點A，C的坐標分別為（-5,1）、（-1,4），結合所給的平面直角坐標系解答下列問題：
畫出△ABC關于
軸對稱的△A1B1C1；
畫出△ABC關于原點O對稱的△A2B2C2；
點C1的坐標是 ；點C2的坐標是 ；
試判斷：△A1B1C1與△A2B2C2是否關于y軸對稱？（只需寫出判斷結果）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩車同時從
地前往
地，甲車先到達地，停留半小時后按原路返回．乙車的行駛速度為每小時50千米．如圖所示是兩車離出發點地的距離
（千米）與行駛時間
（小時）之間的函數圖象．有下列說法：
①、兩地的距離是400千米；
②甲車從到的行駛速度是每小時80千米；
③甲車從到的行駛速度是每小時80千米；
④兩車相遇后1.6小時乙車到達地．
其中正確的說法有（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
