
【題目】△ABC中,BC=12,高AD=8,矩形EFGH的一邊GH在BC上,頂點E、F分別在AB、AC上,AD與EF交于點M.
(1)求證:![]() ;
;
(2)設EF=x,EH=y,寫出y與x之間的函數表達式;
(3)設矩形EFGH的面積為S,求S與x之間的函數表達式,并寫出S的最大值.

【答案】(1)見解析;(2)y=8﹣![]() x(0<x<12);(3)S矩形EFGH=﹣
x(0<x<12);(3)S矩形EFGH=﹣![]() (x﹣6)2+24,Smax=24.
(x﹣6)2+24,Smax=24.
【解析】
(1)先判斷出AM是△AEF的高,再判斷出△AEF∽△ABC,即可得出結論;(2)先判斷出四邊形EMDG是矩形,得出DM=EH,進而表示出AM=8﹣y,借助(1)的結論即可得出結論;(3)由矩形的面積公式得出函數關系式,即可得出結論.
解:(1)∵四邊形EFGH是矩形,
∴EF∥BC,
∵AD是△ABC的高,
∴AD⊥BC,
∴AM⊥EF,
∵EF∥BC,
∴△AEF∽△ABC,
∴![]() (相似三角形的對應邊上高的比等于相似比);
(相似三角形的對應邊上高的比等于相似比);
(2)∵四邊形EFGH是矩形,
∴∠FEH=∠EHG=90°,
∵AD⊥BC,
∴∠HDM=90°=∠FEH=∠EHG,
∴四邊形EMDH是矩形,
∴DM=EH,
∵EF=x,EH=y,AD=8,
∴AM=AD﹣DM=AD﹣EH=8﹣y,
由(1)知,![]() ,
,
∴![]() ,
,
∴y=8﹣![]() x(0<x<12);
x(0<x<12);
(3)由(2)知,y=8﹣![]() x,
x,
∴S=S矩形EFGH=xy=x(8﹣![]() x)=﹣
x)=﹣![]() (x﹣6)2+24,
(x﹣6)2+24,
∵a=﹣![]() <0,
<0,
∴當x=6時,Smax=24.


科目:初中數學 來源: 題型:
【題目】小紅家的陽臺上放置了一個曬衣架如圖①.圖②是曬衣架的側面示意圖,立桿AB,CD相交于點O,B,D兩點立于地面.經測量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,現將曬衣架完全穩固張開,扣鏈EF成一條線段,且EF=32 cm.垂掛在衣架上的連衣裙總長度小于________cm時,連衣裙才不會拖落到地面上.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,⊙O與⊙P相交于A、B兩點,點P在⊙O上,⊙O的弦AC切⊙P于點A,CP及其延長線交⊙P于D、E,過點E作EF⊥CE交CB的延長線于F.
(1)求證:BC是⊙P的切線;
(2)若CD=2,CB=2![]() ,求EF的長.
,求EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:拋物線y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求證:拋物線與x軸有交點;
(2)若拋物線與x軸交于點A(x1,0),B(x2,0),點A在點B的右側,且x1+2x2=1.
①求m的值;
②點P在拋物線上,點G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:①2a+b<0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤(a﹣2b+c)<0,其中正確的個數是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD是一次函數y=x+1圖象的其中一個伴侶正方形.
(1)若某函數是一次函數y=x+1,求它的圖象的所有伴侶正方形的邊長;

(2)若某函數是反比例函數![]() ,它的圖象的伴侶正方形為ABCD,點D(2,m)(m<2)在反比例函數圖象上,求m的值及反比例函數解析式;
,它的圖象的伴侶正方形為ABCD,點D(2,m)(m<2)在反比例函數圖象上,求m的值及反比例函數解析式;

(3)若某函數是二次函數y=ax2+c(a≠0),它的圖象的伴侶正方形為ABCD,C、D中的一個點坐標為(3,4).寫出伴侶正方形在拋物線上的另一個頂點坐標,寫出符合題意的其中一條拋物線解析式,并判斷你寫出的拋物線的伴侶正方形的個數是奇數還是偶數?.(本小題只需直接寫出答案)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一塊長方形鏡面玻璃的四周鑲上與它的周長相等的邊框,制成一面鏡子,鏡子的長與寬的比是2:1,已知鏡面玻璃的價格是每平方米120元,邊框的價格是每米30元,另外制作這面鏡子還需加工費45元.設制作這面鏡子的總費用是![]() 元,鏡子的寬是
元,鏡子的寬是![]() 米.
米.
(1)求![]() 與
與![]() 之間的關系式.
之間的關系式.
(2)如果制作這面鏡子共花了195元,求這面鏡子的長和寬.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,以點O為圓心的圓分別交x軸的正半軸于點M,交y軸的正半軸于點N.劣弧![]() 的長為
的長為![]() ,直線
,直線![]() 與x軸、y軸分別交于點A、B.
與x軸、y軸分別交于點A、B.
(1)求證:直線AB與⊙O相切;
(2)求圖中所示的陰影部分的面積(結果用π表示)
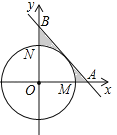
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com