
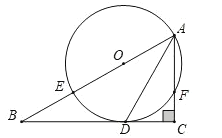
【題目】如圖,E是![]() 的斜邊AB上一點,以AE為直徑的
的斜邊AB上一點,以AE為直徑的![]() 與邊BC相切于點D,交邊AC于點F,連結AD.
與邊BC相切于點D,交邊AC于點F,連結AD.
(1)求證:AD平分![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)連結OD,由切線的性質及∠C=90°可得OD∥AC,進而得∠CAD=∠ODA,再由OA=OD得∠OAD=∠ODA,等量代換即可得證;
(2)先由∠CAD=25°求得∠EOF=100°,再利用弧長公式計算即可.
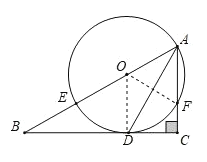
(1)如圖,連結OD.
∵⊙O與邊BC相切于點D,
∴OD⊥BC,
∴∠ODB=90°.
∵∠C=90°,
∴∠C=∠ODB=90°,
∴OD∥AC,
∴∠CAD=∠ODA.
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD.
∴AD平分∠BAC.
(2)如圖,連結OF.
∵AD平分∠BAC,且∠CAD=25°,
∴![]() ,
,
∴∠EOF=100°,
∴![]() 的長為
的長為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖是某隧道截面示意圖,它是由拋物線和長方形構成,已知![]() 米,
米,![]() 米,拋物線頂點D到地面OA的垂直距離為10米,以OA所在直線為x軸,以OB所在直線為y軸建立直角坐標系.
米,拋物線頂點D到地面OA的垂直距離為10米,以OA所在直線為x軸,以OB所在直線為y軸建立直角坐標系.

![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 由于隧道較長,需要在拋物線型拱壁上需要安裝兩排燈,使它們到地面的高度相同,如果燈離地面的高度不超過8米,那么兩排燈的水平距離最小是多少米?
由于隧道較長,需要在拋物線型拱壁上需要安裝兩排燈,使它們到地面的高度相同,如果燈離地面的高度不超過8米,那么兩排燈的水平距離最小是多少米?
![]() 一輛特殊貨運汽車載著一個長方體集裝箱,集裝箱寬為4m,最高處與地面距離為6m,隧道內設雙向行車道,雙向行車道間隔距離為
一輛特殊貨運汽車載著一個長方體集裝箱,集裝箱寬為4m,最高處與地面距離為6m,隧道內設雙向行車道,雙向行車道間隔距離為![]() ,交通部門規定,車載貨物頂部距離隧道壁的豎直距離不少于
,交通部門規定,車載貨物頂部距離隧道壁的豎直距離不少于![]() ,才能安全通行,問這輛特殊貨車能否安全通過隧道?
,才能安全通行,問這輛特殊貨車能否安全通過隧道?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了緩解上學時校門口的交通壓力,某校隨機抽取了部分學生進行了調查,來了解學生的到校方式,并根據調查結果繪制了如下統計圖表:
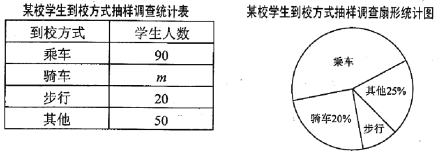
根據統計圖所提供的信息,解答下列問題:
(1)本次抽樣調查中的樣本容量是 ,![]() = .
= .
(2)扇形統計圖中學生到校方式是“步行”所對應扇形的圓心角的度數是 .
(3)若該校共有1500名學生,請根據統計結果估計該校到校方式為“乘車”的學生人數;
(4)現從四名采取不同到校方式的學生中抽取兩名學生進行問卷調查,請你用列表或畫樹狀圖的方法,求出正好選到到校方式為“騎車”和“步行”的兩名學生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國漢代數學家趙爽為了證明勾股定理,創造了一幅“弦圖”后人稱其為“趙爽弦圖”(如圖1).圖2是弦圖變化得到,它是用八個全等的直角三角形拼接而成,記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3,若S1+S2+S3=10,求S2的值.以下是求S2的值的解題過程,請你根據圖形補充完整.
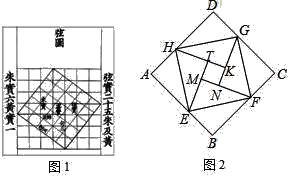
解:設每個直角三角形的面積為S
S1﹣S2= (用含S的代數式表示)①
S2﹣S3= (用含S的代數式表示)②
由①,②得,S1+S3= 因為S1+S2+S3=10,
所以2S2+S2=10.
所以S2=![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定:平面內點A到圖形G上各個點的距離的最小值稱為該點到這個圖形的最小距離d,點A到圖形G上各個點的距離的最大值稱為該點到這個圖形的最大距離D,定義點A到圖形G的距離跨度為R=D-d.
(1)①如圖1,在平面直角坐標系xOy中,圖形G1為以O為圓心,2為半徑的圓,直接寫出以下各點到圖形G1的距離跨度:
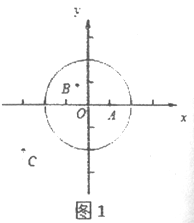
A(1,0)的距離跨度______________;
B(-![]() ,
, ![]() )的距離跨度____________;
)的距離跨度____________;
C(-3,-2)的距離跨度____________;
②根據①中的結果,猜想到圖形G1的距離跨度為2的所有的點組成的圖形的形狀是______________.
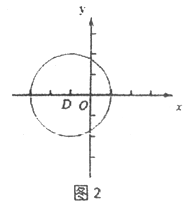
(2)如圖2,在平面直角坐標系xOy中,圖形G2為以D(-1,0)為圓心,2為半徑的圓,直線y=k(x-1)上存在到G2的距離跨度為2的點,求k的取值范圍.
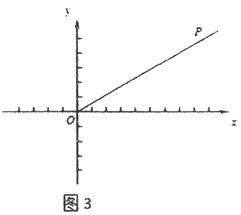
(3)如圖3,在平面直角坐標系xOy中,射線OP:y=![]() x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,求出圓心E的橫坐標xE的取值范圍.
x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,求出圓心E的橫坐標xE的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,對于點P(x,y)和Q(x,y′),給出如下定義:如果y′=![]() ,那么稱點Q為點P的“伴隨點”.
,那么稱點Q為點P的“伴隨點”.
例如:點(5,6)的“伴隨點”為點(5,6);點(﹣5,6)的“伴隨點”為點(﹣5,﹣6).
(1)直接寫出點A(2,1)的“伴隨點”A′的坐標.
(2)點B(m,m+1)在函數y=kx+3的圖象上,若其“伴隨點”B′的縱坐標為2,求函數y=kx+3的解析式.
(3)點C、D在函數y=﹣x2+4的圖象上,且點C、D關于y軸對稱,點D的“伴隨點”為D′.若點C在第一象限,且CD=DD′,求此時“伴隨點”D′的橫坐標.
(4)點E在函數y=﹣x2+n(﹣1≤x≤2)的圖象上,若其“伴隨點”E′的縱坐標y′的最大值為m(1≤m≤3),直接寫出實數n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
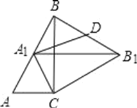
【題目】如圖,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC繞點C順時針旋轉得△A1B1C,當A1落在AB邊上時,連接B1B,取BB1的中點D,連接A1D,則A1D的長度是( )
A.![]() B.
B.![]() C.
C.![]() D.6
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() (點
(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于
軸交于![]() .
.

![]() 求點
求點![]() 的坐標;
的坐標;
![]() 若點
若點![]() 是拋物線在第二象限部分上的一動點,其橫坐標為
是拋物線在第二象限部分上的一動點,其橫坐標為![]() 求
求![]() 為何值時,圖中陰影部分面積最小,并寫出此時點
為何值時,圖中陰影部分面積最小,并寫出此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人加工同一種零件,甲每天加工的數量是乙每天加工數量的 1.5 倍,兩人各加工 600 個這種零件,甲比乙少用 5 天.
(1)求甲、乙兩人每天各加工多少個這種零件?
(2)已知甲、乙兩人加工這種零件每天的加工費分別是 150 元和 120 元,現有 3000 個這種零件的加工任務,甲單獨加工一段時間后另有安排,剩余任務由乙單獨完成.如果總加工費不超過 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com