
【題目】在平面直角坐標系xOy中,⊙O的半徑為r(r>0).給出如下定義:若平面上一點P到圓心O的距離d,滿足![]() ,則稱點P為⊙O的“隨心點”.
,則稱點P為⊙O的“隨心點”.
(1)當⊙O的半徑r=2時,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“隨心點”是 ;
)中,⊙O的“隨心點”是 ;
(2)若點E(4,3)是⊙O的“隨心點”,求⊙O的半徑r的取值范圍;
(3)當⊙O的半徑r=2時,直線y=- x+b(b≠0)與x軸交于點M,與y軸交于點N,若線段MN上存在⊙O的“隨心點”,直接寫出b的取值范圍 .
【答案】(1) A,C ;(2)![]() ;(3) 1≤b≤
;(3) 1≤b≤![]() 或-
或-![]() ≤b≤-1.
≤b≤-1.
【解析】
(1)根據已知條件求出d的范圍:1≤d≤3,再將各點距離O點的距離,進行判斷是否在此范圍內即可,滿足條件的即為隨心點;
(2)根據點E(4,3)是⊙O的“隨心點”,可根據![]() ,求出d=5,再求出r的范圍即可;
,求出d=5,再求出r的范圍即可;
(3)如圖a∥b∥c∥d,⊙O的半徑r=2,求出隨心點范圍![]() ,再分情況點N在y軸正半軸時,當點N在y軸負半軸時,分情況討論即可.
,再分情況點N在y軸正半軸時,當點N在y軸負半軸時,分情況討論即可.
(1) ∵⊙O的半徑r=2,
∴![]() =3,
=3,![]() =1
=1
∴1≤d≤3
∵A(3,0),
∴OA=3,在范圍內
∴點A是⊙O的“隨心點”
∵B(0,4)
∴OB=4,而4>3,不在范圍內
∴B是不是⊙O的“隨心點”,
∵C(![]() ,2),
,2),
∴OC=![]() ,在范圍內
,在范圍內
∴點C是⊙O的“隨心點”,
∵D(![]() ,
,![]() ),
),
∴OD=![]() <1,不在范圍內
<1,不在范圍內
∴點D不是⊙O的“隨心點”,
故答案為:A,C
(2)∵點E(4,3)是⊙O的“隨心點”
∴OE=5,即d=5
若![]() , ∴r=10
, ∴r=10
若 ![]() ,
,![]()
∴![]()
(3)
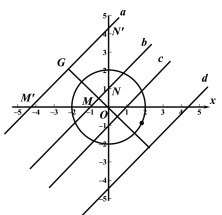
∵如圖a∥b∥c∥d,⊙O的半徑r=2,隨心點范圍![]()
∴![]()
∵直線MN的解析式為y=x+b,
∴OM=ON,
①點N在y軸正半軸時,
當點M是⊙O的“隨心點”,此時,點M(-1,0),
將M(-1,0)代入直線MN的解析式y=x+b中,解得,b=1,
即:b的最小值為1,
過點O作OG⊥M'N'于G,
當點G是⊙O的“隨心點”時,此時OG=3,
在Rt△ON'G中,∠ON'G=45°,
∴GO=3
∴在Rt△GNN’中,![]() =
=![]() =
=![]() =
=![]() ,
,
b的最大值為![]() ,
,
∴1≤b≤![]() ,
,
②當點N在y軸負半軸時,同①的方法得出-![]() ≤b≤-1.
≤b≤-1.
綜上所述,b的取值范圍是:1≤b≤![]() 或-
或-![]() ≤b≤-1.
≤b≤-1.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
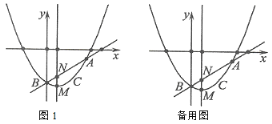
【題目】如圖1,拋物線![]() 過點
過點![]() ,
,![]() ,點
,點![]() 為直線
為直線![]() 下方拋物線上一動點,
下方拋物線上一動點,![]() 為拋物線頂點,拋物線對稱軸與直線
為拋物線頂點,拋物線對稱軸與直線![]() 交于點
交于點![]() .
.
(1)求拋物線的表達式與頂點![]() 的坐標;
的坐標;
(2)在直線![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形,若存在,請求出
為頂點的四邊形是平行四邊形,若存在,請求出![]() 點坐標;
點坐標;
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
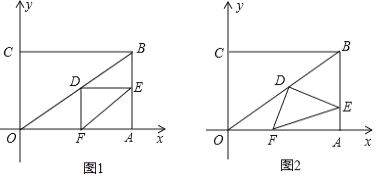
【題目】在直角坐標系中,過原點O及點A(8,0),C(0,6)作矩形OABC,連接OB,點D為OB的中點,點E是線段AB上的動點,連接DE,作DF⊥DE,交OA于點F,連接EF.已知點E從A點出發,以每秒1個單位長度的速度在線段AB上移動,設移動時間為t秒.
(1)如圖1,當t=3時,求DF的長.
(2)如圖2,當點E在線段AB上移動的過程中,![]() 的大小是否發生變化?如果變化,請說明理由;如果不變,請求出
的大小是否發生變化?如果變化,請說明理由;如果不變,請求出![]() 的值.
的值.
(3)連接AD,當AD將△DEF分成的兩部分的面積之比為1:2時,求相應的t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我校八年級有800名學生,在體育中考前進行一次排球模擬測試,從中隨機抽取部分學生,根據其測試成績制作了下面兩個統計圖,請根據相關信息,解答下列問題:

(1)本次抽取到的學生人數為________,圖2中![]() 的值為_________.
的值為_________.
(2)本次調查獲取的樣本數據的平均數是__________,眾數是________,中位數是_________.
(3)根據樣本數據,估計我校八年級模擬體測中得12分的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與函數
與函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,且點
兩點,且點![]() 的坐標為
的坐標為![]() .
.
(1)求![]() 的值;
的值;
(2)已知點![]() ,過點
,過點![]() 作平行于
作平行于![]() 軸的直線,交直線
軸的直線,交直線![]() 于點
于點![]() ,交函數
,交函數![]() 的圖象于點
的圖象于點![]() .
.
①當![]() 時,求線段
時,求線段![]() 的長;
的長;
②若![]() ,結合函數的圖象,直接寫出
,結合函數的圖象,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
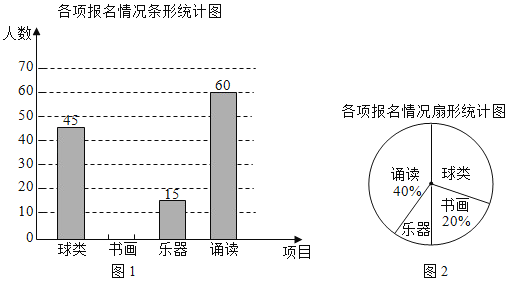
【題目】某校開展以“我們都是追夢人”為主題的校園文化節活動,活動分為球類、書畫、樂器、誦讀四項內容,要求每位學生參加其中的一項.校學生會為了解各項報名情況,隨機抽取了部分學生進行調查,并對調查結果進行了統計,繪制了如下統計圖(均不完整):
請解答以下問題:
(1)圖1中,“書畫”這一項的人數是 .
(2)圖2中,“樂器”這一項的百分比是 ,“球類”這一項所對應的扇形的圓心角度數是 .
(3)若該校共有2200名學生,請估計該校參加“誦讀”這一項的學生約有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
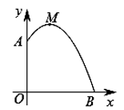
【題目】如圖,某幢建筑物從2.25米高的窗口![]() 用水管向外噴水,噴的水流呈拋物線型(拋物線所在平面與墻面垂直),如果拋物線的最高點
用水管向外噴水,噴的水流呈拋物線型(拋物線所在平面與墻面垂直),如果拋物線的最高點![]() 離墻1米,離地面3米,則水流下落點
離墻1米,離地面3米,則水流下落點![]() 離墻的距離
離墻的距離![]() 是( )
是( )
A.2.5米B.3米C.3.5米D.4米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系內,已知![]() ,過點
,過點![]() 作互相垂直的兩條直線
作互相垂直的兩條直線![]() 、
、![]() ,
, ![]() 分別交
分別交![]() 軸于
軸于![]() 兩點;
兩點;![]() 分別交
分別交![]() 軸于
軸于![]() 兩點,已知
兩點,已知![]() .
.
(1)求![]() 的直線解析式;
的直線解析式;
(2)若點![]() 在
在![]() 軸的負半軸,已知拋物線
軸的負半軸,已知拋物線![]() 的對稱軸經過點
的對稱軸經過點![]() ,拋物線與
,拋物線與![]() 交于對稱軸左側的
交于對稱軸左側的![]() 點,當
點,當![]() 時,求拋物線的函數表達式.
時,求拋物線的函數表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com