
【題目】如圖,在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 和
和![]() 的圖象相交于點
的圖象相交于點![]() ,反比例函數
,反比例函數![]() 的圖象經過點
的圖象經過點![]() .
.
(1)求反比例函數的表達式;
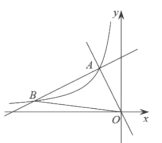
(2)設一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象的另一個交點為
的圖象的另一個交點為![]() ,連接
,連接![]() ,求
,求![]() 的面積.
的面積.
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,BC=4,⊙P與△ABC的邊或邊的延長線相切.若⊙P半徑為2,△ABC的面積為5,則△ABC的周長為( )
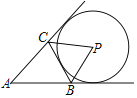
A.8B.10C.13D.14
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,利用我們現在已經學過的圓和銳角三角函數的知識可知,半徑 r 和圓心角θ及其所對的弦長 l之間的關系為![]() ,從而
,從而![]()
![]() ,綜合上述材料當
,綜合上述材料當![]() 時,
時,![]() ______.
______.

查看答案和解析>>
科目:初中數學 來源: 題型:
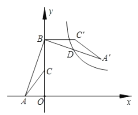
【題目】如圖,點 A 的坐標是(﹣2,0),點 B 的坐標是(0,6),C 為 OB 的中點,將△ABC 繞點 B 逆時針旋轉 90°后得到△A′B′C′.若反比例函數 y ![]() 的圖象恰好經過 A′B 的中點 D,則k _________.
的圖象恰好經過 A′B 的中點 D,則k _________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1和圖2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如圖1,AH⊥BC于點H,則AH=___,AC=___,△ABC的面積![]() =___.
=___.
拓展:如圖2,點D在AC上(可與點A、C重合),分別過點A、C作直線BD的垂線,垂足為E、F,設BD=x,AE=m,CF=n,(當點D與A重合時,我們認為![]() =0).
=0).
(1)用含x、m或n的代數式表示![]() 及
及![]() ;
;
(2)求(m+n)與x的函數關系式,并求(m+n)的最大值和最小值;
(3)對給定的一個x值,有時只能確定唯一的點D,指出這樣的x的取值范圍.
發現:請你確定一條直線,使得A、B、C三點到這條直線的距離之和最小(不必寫出過程),并寫出這個最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:在平面直角坐標系中,任意兩點![]() ,
,![]() 之間的位置關系有以下三種情形;
之間的位置關系有以下三種情形;
①如果![]() 軸,則
軸,則![]() ,
,![]()
②如果![]() 軸,則
軸,則![]() ,
,![]()
③如果![]() 與
與![]() 軸、
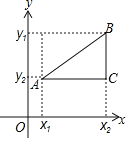
軸、![]() 軸均不平行,如圖,過點
軸均不平行,如圖,過點![]() 作與
作與![]() 軸的平行線與過點
軸的平行線與過點![]() 作與
作與![]() 軸的平行線相交于點
軸的平行線相交于點![]() ,則點
,則點![]() 坐標為
坐標為![]() ,由①得
,由①得![]() ;由②得
;由②得![]() ;根據勾股定理可得平面直角坐標系中任意兩點的距離公式
;根據勾股定理可得平面直角坐標系中任意兩點的距離公式![]() .
.
(1)若點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() 則
則![]() ________;
________;
(2)若點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 是
是![]() 軸上的動點,直接寫出
軸上的動點,直接寫出![]() 最小值=_______;
最小值=_______;
(3)已知![]() ,
,![]() 根據數形結合,求出
根據數形結合,求出![]() 的最小值?
的最小值?![]() 的最大值?
的最大值?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() 的圖象的一支位于第一象限.
的圖象的一支位于第一象限.
(1)判斷該函數圖象的另一支所在的象限,并求m的取值范圍;
(2)如圖,O為坐標原點,點A在該反比例函數位于第一象限的圖象上,點B與點A關于![]() 軸對稱,若△OAB的面積為6,求m的值.
軸對稱,若△OAB的面積為6,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學進行社會調查,隨機抽查了某個小區的200戶家庭的年收入,并繪制成統計圖(如圖).請你根據統計圖給出的信息回答:
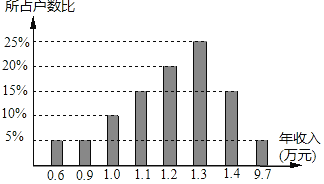
(1)樣本數據的中位數是_____,眾數是_____;
(2)這200戶家庭的平均年收入為_____萬元;
(3)在平均數、中位數兩數中,_____更能反映這個小區家庭的年收入水平.
(4)如果該小區有1200戶住戶,請你根據抽樣調查的結果估計該小區有_____戶家庭的年收入低于1.3萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com