【題目】如圖，AB＝6，O是AB的中點，直線l經過點O，∠1＝120°，P是直線l上一點。當△APB為直角三角形時，AP＝ ．
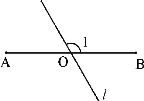
【答案】3或3
或3
．
【解析】
試題分析：分以一下情況討論：
（1）在Rt△A P1B中，∵∠1＝120°，O P1=OB，∴∠O B P1 =∠O P1B=30°，∴AP1 =
AB=×6=3；
（2）在Rt△A P2B中，∵∠1＝120°，O P2=OB，∴∠P2 B O =∠O P2B=60°，∴AP2 =AB=cos∠O B P2×6=
×6=3；
（3）P3B為以B為切點的⊙O的切線，∵∠1＝120°，O P2=OB，∴∠P2 B O =∠O P2B=60°，∴∠P3O B=60°，在Rt△O P3B中，∴BP3 =tan∠P3O B×3 =×3=3;在Rt△A P3B中，AP3 =
=
=3；
（4）P4B為以A為切點的⊙O的切線，∵∠1＝120°，O P1=OA，∴∠P1 A O =∠O P1A=60°，∴∠P4O A=60°，在Rt△O P4A中，∴AP4 =tan∠P4O A×3 =×3=3．
綜上，當△APB為直角三角形時，AP＝3，或3，或3．
科目：初中數學 來源： 題型：
【題目】為“厲行節能減排，倡導綠色出行”，某公司擬在我縣甲、乙兩個街道社區試點投放一批共享單車（俗稱“小黃車”），這批自行車包括A、B兩種不同款型，投放情況如下表：
成本單價 （單位：元） | 投放數量（單位：輛） | 總價（單位：元） | |
A型 |
| 50 | 50 |
B型 |
| 50 |
|
成本合計（單位：元） | 7500 | ||
（1）根據表格填空：
本次試點投放的A、B型“小黃車”共有 輛；用含有
的式子表示出B型自行車的成本總價為 ；
（2）試求A、B兩種款型自行車的單價各是多少元？
（3）經過試點投放調查，現在該公司決定采取如下方式投放A型“小黃車”：甲街區每100人投放n輛，乙街區每100人投放（n+2）輛，按照這種投放方式，甲街區共投放1500輛，乙街區共投放1200輛，如果兩個街區共有
人，求甲街區每100人投放A型“小黃車”的數量．
查看答案和解析>>
科目：初中數學 來源： 題型：
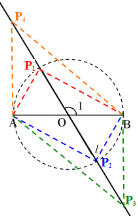
【題目】如圖，直線l1：y＝x+6與直線l2：y＝kx+b相交于點A，直線l1與y軸相交于點B，直線l2與y軸負半軸相交于點C，OB＝2OC，點A的縱坐標為3．
（1）求直線l2的解析式；
（2）將直線l2沿x軸正方向平移，記平移后的直線為l3，若直線l3與直線l1相交于點D，且點D的橫坐標為1，求△ACD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】四邊形ABCD中，對角線AC、BD相交于點O，下列條件不能判定這個四邊形是平行四邊形的是
A．AB∥DC，AD∥BC B．AB=DC，AD=BC
C．AO=CO，BO=DO D．AB∥DC，AD=BC
查看答案和解析>>
科目：初中數學 來源： 題型：
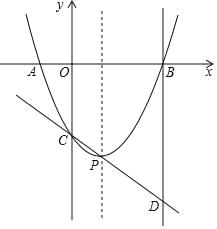
【題目】如圖，二次函數 y＝ax2﹣2ax+c(a＞0)的圖象與 x 軸的負半軸和正半軸分別交于 A、B 兩點，與 y 軸交于點 C，它的頂點為 P，直線 CP 與過點B 且垂直于 x 軸的直線交于點 D，且 CP：PD＝1：2，tan∠PDB＝
．
(1)則 A、B 兩點的坐標分別為 A( ， )； B( ， )；
(2)求這個二次函數的解析式；
(3)在拋物線的對稱軸上找一點M 使|MC﹣MB|的值最大，則點M 的坐標為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
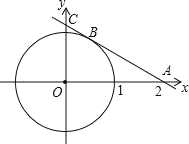
【題目】如圖，圓 O 的半徑為 1，過點 A(2，0)的直線與圓 O 相切于點 B，與 y 軸相交于點 C．
(1)求 AB 的長；
(2)求直線 AB 的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數 y＝ax2﹣2ax+c(a＞0)的圖象與 x 軸的負半軸和正半軸分別交于 A、B 兩點，與 y 軸交于點 C，它的頂點為 P，直線 CP 與過點B 且垂直于 x 軸的直線交于點 D，且 CP：PD＝1：2，tan∠PDB＝
．
(1)則 A、B 兩點的坐標分別為 A( ， )； B( ， )；
(2)求這個二次函數的解析式；
(3)在拋物線的對稱軸上找一點M 使|MC﹣MB|的值最大，則點M 的坐標為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD中，AB=6，AD=2
，將矩形ABCD繞點B按順時針方向旋轉后得到矩形EBGF，此時恰好四邊形AEHB為菱形，連接CH交FG于點M，則HM的長度為（ ）
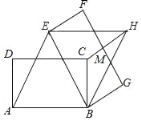
A. 
B. 2 C. 
D. 1
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在一個不透明的袋子中裝有除顏色外其余均相同的m個小球，其中 5 個黑球， 從袋中隨機摸出一球，記下其顏色，這稱為依次摸球試驗，之后把它放回袋 中，攪勻后，再繼續摸出一球．以下是利用計算機模擬的摸球試驗次數與摸出黑球次數的列表：
摸球試驗次數 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次數 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根據列表，可以估計出 m 的值是（ ）
A. 5 B. 10 C. 15 D. 20
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
