
【題目】已知正方形![]() 內接于
內接于![]() ,點
,點![]() 為
為![]() 上一點,連接
上一點,連接![]() 、
、![]() 、
、![]() .
.
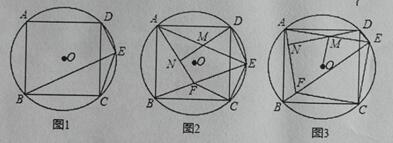
(1)如圖1,求證:∠DEC+∠BEC= 180°;
(2)如圖2,過點C作CF⊥CE交BE于點F,連接AF, M為AE的中點,連接DM并延長交AF于點N,求證: DN⊥AF;
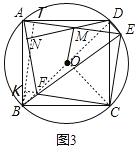
(3)如圖3,在(2) 的條件下,連接OM,若AB=10,![]() 求OM的長.
求OM的長.
【答案】(1)證明過程見解析;(2)證明過程見解析;(3)![]() ;
;
【解析】
(1)連接BD,OC,得出∠BEC=45°,由圓周角定理可得出結論
(2)延長ED至G,使ED=DG,連接AG,證明△BFC≌△DEC,可得出BF=DE,證明△ABF≌△ADG,則∠BAF=∠DAC,證明DM∥AG,得出∠DNF=∠FAG=90°,則可得出結論;
(3)連接BD,OC,過點B作BK⊥CF交CF的延長線于點K,過點B作BT⊥AE于點T,設DE=x,則BE=7x,得出BD=5![]() x,求出x=2,求出BK=KF=
x,求出x=2,求出BK=KF=![]() ,由tan∠BCF=tan∠DCE=
,由tan∠BCF=tan∠DCE=![]() ,求出CF,可求出TB=7
,求出CF,可求出TB=7![]() ,AM=4
,AM=4![]() ,則可求出OM的長.
,則可求出OM的長.
解:(1)證明:連接BD,OC,
∵四邊形ABCD為正方形,
∴∠A=90°,BC= CD,
∴BD為⊙O的直徑,即∠DEB=90°,
∵OB= OD,
∴OC⊥BD,即∠BOC= 90°,
∴∠BEC=![]() ∠ BOC=45°,
∠ BOC=45°,
∴∠DEC+∠BEC=∠DEB+∠BEC+∠BEC= 180°.
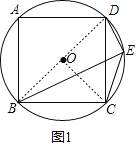
(2)證明:如圖,延長ED至G,使ED=DG,連接AG,
∵CE⊥CF,∴∠ECF=90°,
∵∠CEF=45°,
∴∠CEF=∠CFE=45°,
∴CE= CF,
∵∠BCD=∠ECF=90°,
∴∠BCF=∠DCE,
∵BC=CD,
∴△BFC≌ODEC (SAS),即BF=DE ,
∵DE=DG,
∴BF=DG,
∵四邊形ABED為圓O的內接四邊形,
∴∠ABE+∠ADE= 180°,
∴∠ADE+∠ADG=180°,
∴∠ABE=∠ADG,
∵AB=AD,
∴△ABF≌OADG (SAS), 即∠BAF=∠DAG,
∵∠BAF+∠FAD=∠BAD=90°,
∴∠DAG+∠FAD=90°,即∠FAG= 90°.
∵M為AE的中點,
∴DM為△AEG的中位線,即DM// AG,
∴∠DNF=∠FAG=90°,即DN⊥AF.
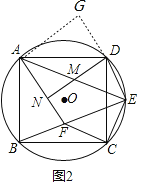
(3)解:如圖,連接BD,OC,過B作BK⊥CF的延長線于點K,
過點B作BT⊥AE于T,
由(1)知![]() ,則
,則![]() ,
,
由(1)知BD為⊙O的直徑,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
設DE=x,則BE=7x,
在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
由(2)知![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() 為
為![]() 的中點,∴
的中點,∴![]() ,
,
在![]() 中,
中,![]() .
.


科目:初中數學 來源: 題型:
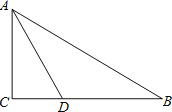
【題目】已知:如圖,在![]() 中,
中,![]() 的角平分線
的角平分線![]() 交
交![]() 邊于
邊于![]() .
.
(1)以![]() 邊上一點
邊上一點![]() 為圓心,過
為圓心,過![]() 兩點作
兩點作![]() (不寫作法,保留作圖痕跡),再判斷直線
(不寫作法,保留作圖痕跡),再判斷直線![]() 與
與![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)若(1)中的![]() 與
與![]() 邊的另一個交點為
邊的另一個交點為![]() ,
,![]() ,求線段
,求線段![]() 與劣弧
與劣弧![]() 所圍成的圖形面積.(結果保留根號和
所圍成的圖形面積.(結果保留根號和![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某報社為了解市民對“社會主義核心價值觀”的知曉程度,采取隨機抽樣的方式進行問卷調查,調查結果分為“A.非常了解”、“B.了解”、“C.基本了解”三個等級,并根據調查結果繪制了如下兩幅不完整的統計圖.
(1)這次調查的市民人數為________人,m=________,n=________;
(2)補全條形統計圖;
(3)若該市約有市民100000人,請你根據抽樣調查的結果,估計該市大約有多少人對“社會主義核心價值觀”達到“A.非常了解”的程度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的網格中,![]() 的頂點A,B,O均落在格點上,
的頂點A,B,O均落在格點上,![]() 為⊙O的半徑.
為⊙O的半徑.
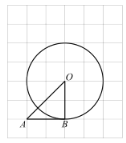
(1)![]() 的大小等于_________(度);
的大小等于_________(度);
(2)將![]() 繞點O順時針旋轉,得
繞點O順時針旋轉,得![]() ,點A,B旋轉后的對應點為
,點A,B旋轉后的對應點為![]() ,
,![]() .連接
.連接![]() ,設線段
,設線段![]() 的中點為M,連接
的中點為M,連接![]() .當
.當![]() 取得最大值時,請在如圖所示的網格中,用無刻度的直尺畫出點
取得最大值時,請在如圖所示的網格中,用無刻度的直尺畫出點![]() ,并簡要說明點
,并簡要說明點![]() 的位置是如何找到的(不要求證明).
的位置是如何找到的(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
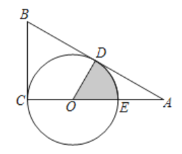
【題目】如圖,O為Rt△ABC直角邊AC上一點,以OC為半徑作⊙O與斜邊AB相切于點D,交OA于點E,已知![]() ,AC=3,則圖中陰影部分的面積是__________.
,AC=3,則圖中陰影部分的面積是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
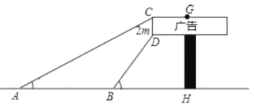
【題目】數學小組想利用所學的知識了解某廣告牌的高度(圖中![]() 的長),經測量知
的長),經測量知![]() ,在B處測得點D的仰角為
,在B處測得點D的仰角為![]() ,在A處測得點C的仰角為
,在A處測得點C的仰角為![]() ,
,![]() ,且A、B、H三點在一條直線上,請根據以上數據計算GH的長(
,且A、B、H三點在一條直線上,請根據以上數據計算GH的長(![]() ,要求結果精確得到0.1
,要求結果精確得到0.1![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小雨、小華、小星暑假到某超市參加社會實踐活動,在活動中他們參加了某種水果的銷售工作,已知該水果的進價為8元/千克.他們通過市場調查發現:當銷售單價為10元時,那么每天可售出300千克;銷售單價每上漲1元,每天的銷售量就減少50千克.
(1)求該超市銷售這種水果,每天的銷售量y(千克)與銷售單價x(元/千克)之間的函數關系式;
(2)一段時間后,發現這種水果每天的銷售量均不低于250千克,則此時該超市銷售這種水果每天獲取的利潤w(元)最大是多少?
(3)為響應政府號召,該超市決定在暑假期間每銷售1千克這種水果就捐贈a元利潤(a≤2.5)給希望工程.公司通過銷售記錄發現,當銷售單價不超過13元時,每天扣除捐贈后的日銷售利潤隨銷售單價x(元/千克)的增大而增大,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線與x軸交于A(-1,0)和B(3,0)兩點,且與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)拋物線的對稱軸方程和頂點M坐標;
(3)求四邊形ABMC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解市民對“垃圾分類知識”的知曉程度,某數學學習興趣小組對市民進行 隨機抽樣的問卷調查,調查結果分為“A.非常了解”、“B.了解”、“C.基本了解”、“D.不太了解”四個等級進行統計,并將統計結果繪制成如下兩幅不完整的統計圖(圖1,圖2), 請根據圖中的信息解答下列問題.
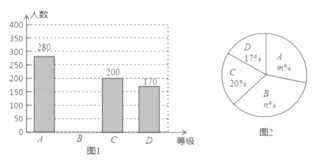
(1)這次調查的市民人數為________人,圖2中,![]() _________;
_________;
(2)圖1中的條形統計圖中B等級的人數;
(3)在圖2中的扇形統計圖中,求“C.基本了解”所在扇形的圓心角度數;
(4)據統計,2018年該市約有市民500萬人,那么根據抽樣調查的結果,可估計對“垃圾分類知識”的知曉程度為“A.非常了解”的市民約有多少萬人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com