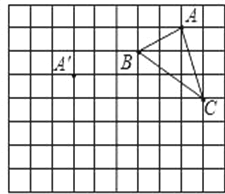
【題目】在正方形網格中，每個小正方形的邊長均為1個單位長度，
的三個頂點的位置如圖所示，現將平移，使點A變換為點A′，點B′,C′,分別是B,C的對應點．
（1）請畫出平移后的
，并求的面積；
（2）試說明△A'B'C'是如何由△ABC平移得到的；
（3）若連接AA′，CC′，則這兩條線段之間的關系是 ．
快樂小博士鞏固與提高系列答案科目：初中數學 來源： 題型：
【題目】已知12箱蘋果，以每箱10千克為標準，超過10千克的數記為正數，不足10千克的數記為負數，稱重記錄如下：
+0.2 ，—0.2，+0. 7，—0.3，—0.4，+0.6，0，—0.1，—0.6，+0.5，—0.2，—0.5。
⑴求12箱蘋果的總重量；
⑵若每箱蘋果的重量標準為10
0.5（千克），則這12箱有幾箱不合乎標準的？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=x2+bx+c（b，c為常數）．
（1）當b=2，c=﹣3時，求二次函數圖象的頂點坐標；
（2）當c=10時，若在函數值y=1的情況下，只有一個自變量x的值與其對應，求此時二次函數的解析式；
（3）當c=b2時，若在自變量x的值滿足b≤x≤b+3的情況下，與其對應的函數值y的最小值為21，求此時二次函數的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】湖州素有魚米之鄉之稱，某水產養殖大戶為了更好地發揮技術優勢，一次性收購了 
淡水魚，計劃養殖一段時間后再出售．已知每天放養的費用相同，放養 
天的總成本為 
萬元；放養 
天的總成本為 
萬元（總成本=放養總費用+收購成本）．
（1）設每天的放養費用是 
萬元，收購成本為 
萬元，求 和 的值；
（2）設這批淡水魚放養 
天后的質量為 
（ ），銷售單價為 
元/ ．根據以往經驗可知： 與 的函數關系為 
； 與 的函數關系如圖所示．
①分別求出當 
和 
時， 與 的函數關系式；
②設將這批淡水魚放養 天后一次性出售所得利潤為 
元，求當 為何值時， 最大？并求出最大值．（利潤=銷售總額-總成本）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(1)方法回顧：在學習三角形中位線時，為了探索三角形中位線的性質，思路如下：
第一步添加輔助線：如圖1，在
中，延長
（分別是
的中點）到點
，使得
，連接
；
第二步證明
，再證四邊形
是平行四邊形，從而得出三角形中位線的性質結論：____________________________________（請用DE與BC表示）
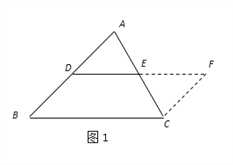
（2）問題解決：如圖2，在正方形ABCD中，E為AD的中點，G、F分別為AB、CD邊上的點，若AG＝2，DF＝3，∠GEF＝90°，求GF的長．
（3）拓展研究：如圖3，在四邊形ABCD中，∠A＝105°，∠D＝120°，E為AD的中點，G、F分別為AB、CD邊上的點，若AG＝
，DF＝2，∠GEF＝90°，求GF的長．
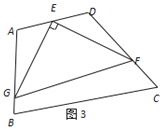
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：如圖1，拋物線 
與 
軸交于A，B兩點，點P在拋物線上（點P與A，B兩點不重合），如果△ABP的三邊滿足 
，則稱點P為拋物線 的勾股點。
（1）直接寫出拋物線 
的勾股點的坐標；
（2）如圖2，已知拋物線C： 
與 軸交于A，B兩點，點P（1， 
）是拋物線C的勾股點，求拋物線C的函數表達式；
（3）在（2）的條件下，點Q在拋物線C上，求滿足條件 
的點Q（異于點P）的坐標
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知數軸上三點M，O，N對應的數分別為－1，0，3，點P為數軸上任意一點，其對應的數為x．
（1）MN的長為 ；
（2）如果點P到點M、點N的距離相等，那么x的值是 ；
（3）數軸上是否存在點P，使點P到點M、點N的距離之和是8？若存在，直接寫出x的值；若不存在，請說明理由．
（4）如果點P以每分鐘1個單位長度的速度從點O向左運動，同時點M和點N分別以每分鐘2個單位長度和每分鐘3個單位長度的速度也向左運動．設t分鐘時點P到點M、點N的距離相等，求t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，如圖A、B分別為數軸上的兩點，A點對應的數為-10，B點對應的數為90．
（1）請寫出與A，B兩點距離相等的M點對應的數；
（2）現在有一只電子螞蟻P從B點出發時，以3個單位/秒的速度向左運動，同時另一只電子螞蟻Q恰好從A點出發，以2個單位/秒的速度向右運動，設兩只電子螞蟻在數軸上的C點相遇，求C點對應的數是多少.
（3）若當電子螞蟻P從B點出發時，以3個單位/秒的速度向左運動，同時另一只電子螞蟻Q恰好從A點出發，以2個單位/秒的速度向右運動，求經過多長的時間兩只電子螞蟻在數軸上相距35個單位長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著手機的普及，微信
一種聊天軟件
的興起，許多人抓住這種機會，做起了“微商”，很多農產品也改變了原來的銷售模式，實行了網上銷售，這不剛大學畢業的小明把自家的冬棗產品也放到了網上，他原計劃每天賣100斤冬棗，但由于種種原因，實際每天的銷售量與計劃量相比有出入，下表是某周的銷售情況超額記為正，不足記為負
單位：斤；
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
與計劃量的差值 |
|
|
|
|
|
|
|
(1)根據記錄的數據可知前三天共賣出 ______ 斤；
(2)根據記錄的數據可知銷售量最多的一天比銷售量最少的一天多銷售 ______ 斤；
(3)本周實際銷售總量達到了計劃數量沒有？
(4)若冬季每斤按8元出售，每斤冬棗的運費平均3元，那么小明本周一共收入多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
