
【題目】如圖,二次函數(shù)![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() ,
,![]() (
(![]() 在
在![]() 左側(cè)),與
左側(cè)),與![]() 軸正半軸交于點
軸正半軸交于點![]() ,點
,點![]() 在拋物線上,
在拋物線上,![]() 軸,且
軸,且![]() .
.
(1)求點![]() ,
,![]() 的坐標及
的坐標及![]() 的值;
的值;
(2)點![]() 為
為![]() 軸右側(cè)拋物線上一點.
軸右側(cè)拋物線上一點.
①如圖①,若![]() 平分
平分![]() ,
,![]() 交
交![]() 于點
于點![]() ,求點
,求點![]() 的坐標;
的坐標;
②如圖②,拋物線上一點![]() 的橫坐標為2,直線
的橫坐標為2,直線![]() 交
交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)令y=0,解方程即可求出點A、B的坐標,由此可求得AB的長及對稱軸,再根據(jù)![]() 即可求得OD長,根據(jù)對稱軸即可求得CD=6,再根據(jù)勾股定理即可求得點C坐標,將點C坐標代入函數(shù)關(guān)系式從而可求得a的值;
即可求得OD長,根據(jù)對稱軸即可求得CD=6,再根據(jù)勾股定理即可求得點C坐標,將點C坐標代入函數(shù)關(guān)系式從而可求得a的值;
(2)①作![]() 于
于![]() ,根據(jù)
,根據(jù)![]() 平分
平分![]() 可得
可得![]() ,進而設(shè)
,進而設(shè)![]() ,根據(jù)
,根據(jù)![]() 可得方程
可得方程![]() 求解即可求得點E坐標為
求解即可求得點E坐標為![]() ,再用待定系數(shù)法求得直線OP的函數(shù)關(guān)系式,與二次函數(shù)關(guān)系式聯(lián)立方程組即可求得點P坐標;
,再用待定系數(shù)法求得直線OP的函數(shù)關(guān)系式,與二次函數(shù)關(guān)系式聯(lián)立方程組即可求得點P坐標;
②分兩種情形(Ⅰ)若點![]() 在
在![]() 點上方,如圖②,(Ⅱ)若點
點上方,如圖②,(Ⅱ)若點![]() 在點
在點![]() 下方,如圖③,分別列出方程即可解決.
下方,如圖③,分別列出方程即可解決.
解:(1)令![]() ,則
,則![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,拋物線的對稱軸為直線
,拋物線的對稱軸為直線![]() ,
,
∵![]()
∴![]() ,
,
∵點C在y軸上且![]() 軸,
軸,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴點![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①作![]() 于
于![]() ,
,
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
設(shè)![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
設(shè)![]() 對應(yīng)函數(shù)表達式為
對應(yīng)函數(shù)表達式為![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
∴![]() 對應(yīng)函數(shù)表達式為
對應(yīng)函數(shù)表達式為![]() .
.
∵![]() ,
,
∴二次函數(shù)表達式為![]() ,
,
∴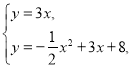 ,
,
解得![]() 或
或![]() (舍去)
(舍去)
∴點![]() .
.
②∵當(dāng)![]() 時,
時,![]() ,∴點
,∴點![]() .
.
設(shè)直線![]() 的函數(shù)表達式為
的函數(shù)表達式為![]()
把點![]() 、點
、點![]() 代入,
代入,
得![]()
解得![]()
∴直線![]() 的函數(shù)表達式為
的函數(shù)表達式為![]() ,
,
∴點![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅰ)若點![]() 在
在![]() 點上方,如圖②.
點上方,如圖②.
過點![]() 作
作![]() 軸的平行線,交
軸的平行線,交![]() 軸于點
軸于點![]() .
.
∵![]() ,
,
∴![]() 軸,
軸,
∵![]() 軸,
軸,
∴點![]() 與點
與點![]() 重合,
重合,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴設(shè)![]() ,
,![]() ,
,
∵![]() 軸,
軸,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴![]() .
.
把![]() 代入
代入![]()
得,![]() .
.
∴![]() .
.
(Ⅱ)若點![]() 在點
在點![]() 下方,如圖③.
下方,如圖③.
過點![]() 作
作![]() 軸,交
軸,交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,交
,交![]() 軸于點
軸于點![]() .
.
∴![]() ,
,
∴四邊形![]() 是正方形,
是正方形,
∴![]()
∵![]() 軸,
軸,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴設(shè)![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() ,得
,得
![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
代入![]() 得
得
![]() ,
,
∴![]() .
.
綜上所述,![]() 或
或![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
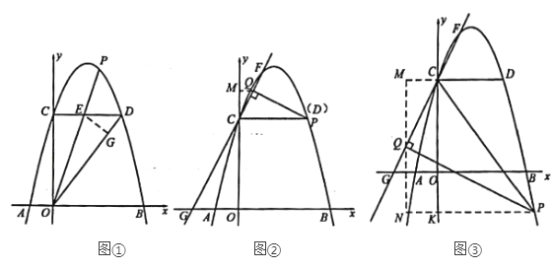
【題目】如圖,已知∠ABM=30°,AB=20,C是射線BM上一點.
(1)在下列條件中,可以唯一確定BC長的是 ;(填寫所有符合條件的序號)
①AC=13;②tan∠ACB=![]() ;③△ABC的面積為126.
;③△ABC的面積為126.
(2)在(1)的答案中,選擇一個作為條件,畫出示意圖,求BC的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
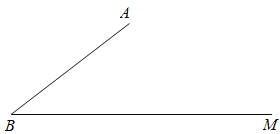
【題目】如圖,在Rt△ABC中,∠BAC=90°,AB=AC.點D為BC中點,E為邊AB上一動點(不與A、B點重合),以點D為直角頂點、以射線DE為一邊作∠MDN=90°,另一條邊DN與邊AC交于點F.下列結(jié)論中正確結(jié)論是( )
①BE=AF;
②△DEF是等腰直角三角形;
③無論點E、F的位置如何,總有EF=DF+CF成立;
④四邊形AEDF的面積隨著點E、F的位置不同發(fā)生變化.
A.①③B.②③C.①②D.①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
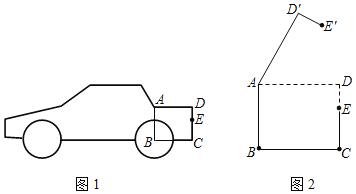
【題目】圖1是某小型汽車的側(cè)面示意圖,其中矩形ABCD表示該車的后備箱,在打開后備箱的過程中,箱蓋ADE可以繞點A逆時針方向旋轉(zhuǎn),當(dāng)旋轉(zhuǎn)角為60°時,箱蓋ADE落在AD′E′的位置(如圖2所示).已知AD=96厘米,DE=28厘米,EC=42厘米.
(1)求點D′到BC的距離;
(2)求E、E′兩點的距離.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】初三(1)班針對“垃圾分類”知曉情況對全班學(xué)生進行專題調(diào)查活動,對“垃圾分類”的知曉情況分為![]() 、
、![]() 、
、![]() 、
、![]() 四類.其中,
四類.其中,![]() 類表示“非常了解”,
類表示“非常了解”,![]() 類表示“比較了解”,
類表示“比較了解”,![]() 類表示“基本了解”,
類表示“基本了解”,![]() 類表示“不太了解”,每名學(xué)生可根據(jù)自己的情況任選其中一類,班長根據(jù)調(diào)查結(jié)果進行了統(tǒng)計,并繪制成了不完整的條形統(tǒng)計圖和扇形統(tǒng)計圖.
類表示“不太了解”,每名學(xué)生可根據(jù)自己的情況任選其中一類,班長根據(jù)調(diào)查結(jié)果進行了統(tǒng)計,并繪制成了不完整的條形統(tǒng)計圖和扇形統(tǒng)計圖.
“垃圾分類”知曉情況各類別人數(shù)條形統(tǒng)計圖 “垃圾分類”知曉情況各類別人數(shù)扇形統(tǒng)計圖

根據(jù)以上信息解決下列問題:
(1)初三(1)班參加這次調(diào)查的學(xué)生有______人,扇形統(tǒng)計圖中類別![]() 所對應(yīng)扇形的圓心角度數(shù)為______°;
所對應(yīng)扇形的圓心角度數(shù)為______°;
(2)求出類別![]() 的學(xué)生數(shù),并補全條形統(tǒng)計圖;
的學(xué)生數(shù),并補全條形統(tǒng)計圖;
(3)類別![]() 的4名學(xué)生中有2名男生和2名女生,現(xiàn)從這4名學(xué)生中隨機選取2名學(xué)生參加學(xué)校“垃圾分類”知識競賽,請用列舉法(畫樹狀圖或列表)求所選取的2名學(xué)生中恰好有1名男生、1名女生的概率.
的4名學(xué)生中有2名男生和2名女生,現(xiàn)從這4名學(xué)生中隨機選取2名學(xué)生參加學(xué)校“垃圾分類”知識競賽,請用列舉法(畫樹狀圖或列表)求所選取的2名學(xué)生中恰好有1名男生、1名女生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
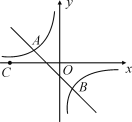
【題目】如圖,點A(-2,n),B(1,-2)是一次函數(shù)y=kx+b的圖象和反比例函數(shù)y=![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求反比例函數(shù)和一次函數(shù)的解析式;
(2)根據(jù)圖象寫出,當(dāng)kx+b<![]() 時,x的取值范圍;
時,x的取值范圍;
(3)若C是x軸上一動點,設(shè)t=CB-CA,求t的最大值,并求出此時點C的坐標.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】龍蝦狂歡季再度開啟,第![]() 屆中國合肥龍蝦節(jié)的主題是“讓你知蝦,也知稻”,稻田小龍蝦養(yǎng)殖技術(shù)在合肥周邊的鄉(xiāng)鎮(zhèn)大力推廣,已知每千克小龍蝦養(yǎng)殖成本為
屆中國合肥龍蝦節(jié)的主題是“讓你知蝦,也知稻”,稻田小龍蝦養(yǎng)殖技術(shù)在合肥周邊的鄉(xiāng)鎮(zhèn)大力推廣,已知每千克小龍蝦養(yǎng)殖成本為![]() 元,在整個銷售旺季的
元,在整個銷售旺季的![]() 天里,銷售單價
天里,銷售單價![]() 元/千克,與時間
元/千克,與時間![]() (天)之間的函數(shù)關(guān)系式為:
(天)之間的函數(shù)關(guān)系式為: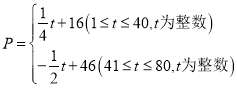 ,日銷售量
,日銷售量![]() (千克)與時間第
(千克)與時間第![]() (天)之間的函數(shù)關(guān)系如圖所示:
(天)之間的函數(shù)關(guān)系如圖所示:
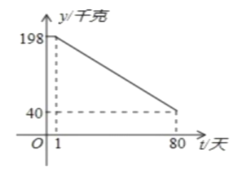
(1)求日銷售量![]() 與時間
與時間![]() 的函數(shù)關(guān)系式?
的函數(shù)關(guān)系式?
(2)哪一天的日銷售利潤最大?最大利潤是多少?
(3)在實際銷售的前![]() 天中,該養(yǎng)殖戶決定銷售
天中,該養(yǎng)殖戶決定銷售![]() 千克小龍蝦,就捐贈
千克小龍蝦,就捐贈![]() 元給村里的特困戶,在這前
元給村里的特困戶,在這前![]() 天中,每天扣除捐贈后的日銷售利潤隨時間
天中,每天扣除捐贈后的日銷售利潤隨時間![]() 的增大而增大,求
的增大而增大,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,菱形ABCD的邊長為6,∠B=120°.點P是對角線AC上一點(不與端點A重合),則![]() AP+PD的最小值為_____.
AP+PD的最小值為_____.
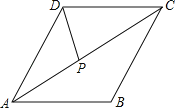
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,過邊長為3的等邊△ABC的邊AB上一點P,作PE⊥AC于E,Q為BC延長線上一點,當(dāng)PA=CQ時,連PQ交AC邊于D,則DE的長為_____.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com