
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,
,![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() .則以下結(jié)論:①
.則以下結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,⑤
,⑤![]() ,其中正確的結(jié)論有( )
,其中正確的結(jié)論有( )
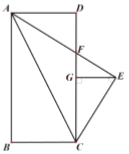
A.1個(gè)B.2個(gè)C.3個(gè)D.4個(gè)
【答案】D
【解析】
過(guò)點(diǎn)F作FH⊥AC,由角平分線的性質(zhì)得到HF=DF,延長(zhǎng)CE與AD的延長(zhǎng)線交于點(diǎn)M,
又AF平分∠CAD,AF⊥CE,由“三線合一”逆定理,得到AC=AM,CE=EM.再設(shè)HF=DF=x,由等積法得到![]() ,從而求出關(guān)鍵的DF的值.利用勾股定理得到AC=AH=
,從而求出關(guān)鍵的DF的值.利用勾股定理得到AC=AH=![]() , 有DM=
, 有DM=![]() ,
,![]() ,所以CE=
,所以CE=![]() ,而后找到圖中常見的相識(shí)三角形并利用其性質(zhì)逐一推理計(jì)算判斷即可.
,而后找到圖中常見的相識(shí)三角形并利用其性質(zhì)逐一推理計(jì)算判斷即可.
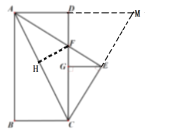
解:∵∠CEF=∠CEA=90°,∠CAE=∠EAD=∠FCE,
∴![]() ;
;
故① 對(duì);
若![]() 成立,則易知∠BAC=∠EAC=∠FAD=30°,則在
成立,則易知∠BAC=∠EAC=∠FAD=30°,則在![]() 中BC=
中BC=![]() AB,而BC=2,AB=4,BC=
AB,而BC=2,AB=4,BC=![]() AB,故假設(shè)不成立. ②不對(duì);
AB,故假設(shè)不成立. ②不對(duì);
過(guò)點(diǎn)F作FH⊥AC,∵AF平分∠CAD,AD⊥DF,∴HF=DF=x,則CF=4-x,
又∵![]() ,
,
∵![]() ,
,
∴![]()
解得![]()
∴![]() ,
, ![]() ∴
∴![]() ,故④對(duì);
,故④對(duì);
又∵![]() ,
,
延長(zhǎng)CE與AD的延長(zhǎng)線交于點(diǎn)M,
∵AF平分∠CAD,AF⊥CE,
∴AC=AM=![]() ,CE=EM=
,CE=EM=![]() ,
,
∴DM=![]() ,又∵
,又∵![]()
∴![]()
∴![]() ,故③對(duì);
,故③對(duì);
∵∠CGE=∠ADF=90°,∠ECG=∠DAF,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CG=DG=2,
又∵∠FEC=90°,GE⊥CF,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴ ![]() ,又∵CG=DG,
,又∵CG=DG,
∴![]() ∴⑤對(duì);
∴⑤對(duì);
綜上有4個(gè)正確,
故選:D.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1是長(zhǎng)方體模型,棱長(zhǎng)如圖所示,圖2是它的一種表面展開圖.
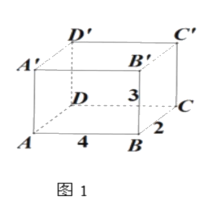
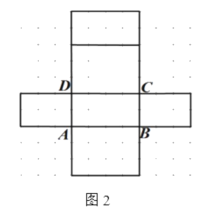

(1)①在圖2中,表示出C可能的位置;
②在圖3中畫出長(zhǎng)方體的一種展開圖(不同于圖2);
(2)圖1中,一只在頂點(diǎn)A的螞蟻,要吃到C處的甜食,求它沿長(zhǎng)方體表面爬行的最短距離;
(3) 在滿足AB+BC+BB=9的條件下,當(dāng)AB為何值時(shí),螞蟻從A沿長(zhǎng)方體表面爬行到C距離最短,并寫出其中的一種方案.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
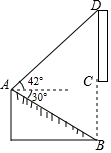
【題目】小婷在放學(xué)路上,看到隧道上方有一塊宣傳“中國(guó)﹣南亞博覽會(huì)”的豎直標(biāo)語(yǔ)牌CD.她在A點(diǎn)測(cè)得標(biāo)語(yǔ)牌頂端D處的仰角為42°,測(cè)得隧道底端B處的俯角為30°(B,C,D在同一條直線上),AB=10m,隧道高6.5m(即BC=65m),求標(biāo)語(yǔ)牌CD的長(zhǎng)(結(jié)果保留小數(shù)點(diǎn)后一位).(參考數(shù)據(jù):sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
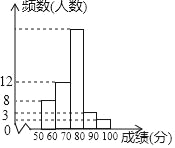
【題目】(7分)某中學(xué)1000名學(xué)生參加了”環(huán)保知識(shí)競(jìng)賽“,為了了解本次競(jìng)賽成績(jī)情況,從中抽取了部分學(xué)生的成績(jī)(得分取整數(shù),滿分為100分)作為樣本進(jìn)行統(tǒng)計(jì),并制作了如圖頻數(shù)分布表和頻數(shù)分布直方圖(不完整且局部污損,其中“■”表示被污損的數(shù)據(jù)).請(qǐng)解答下列問(wèn)題:
成績(jī)分組 | 頻數(shù) | 頻率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合計(jì) | ■ | 1 |
(1)寫出a,b,c的值;
(2)請(qǐng)估計(jì)這1000名學(xué)生中有多少人的競(jìng)賽成績(jī)不低于70分;
(3)在選取的樣本中,從競(jìng)賽成績(jī)是80分以上(含80分)的同學(xué)中隨機(jī)抽取兩名同學(xué)參加環(huán)保知識(shí)宣傳活動(dòng),求所抽取的2名同學(xué)來(lái)自同一組的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,D、E分別是AB、AC的中點(diǎn),BE=2DE,延長(zhǎng)DE到點(diǎn)F,使得EF=BE,連接CF.

(1)求證:四邊形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】初三第一輪復(fù)習(xí)重在查漏補(bǔ)缺,課后很重要的一項(xiàng)任務(wù)是“糾錯(cuò)”.在深大附中九年級(jí)隨機(jī)抽取部分學(xué)生進(jìn)行調(diào)查,對(duì)平時(shí)的錯(cuò)題:![]() 表示“每一道錯(cuò)題都解決了”,
表示“每一道錯(cuò)題都解決了”,![]() 表示“大部分錯(cuò)題解決了”,
表示“大部分錯(cuò)題解決了”,![]() 表示“只有一部分錯(cuò)題解決了”,
表示“只有一部分錯(cuò)題解決了”,![]() 表示“從不解決錯(cuò)題”.對(duì)抽取的學(xué)生問(wèn)卷統(tǒng)計(jì)后如圖:
表示“從不解決錯(cuò)題”.對(duì)抽取的學(xué)生問(wèn)卷統(tǒng)計(jì)后如圖:
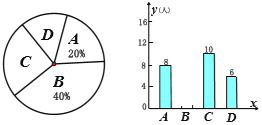
(1)抽查的學(xué)生有______人;扇形統(tǒng)計(jì)圖中,![]() 占比_______;
占比_______;![]() 占比_______.
占比_______.
(2)補(bǔ)全條形統(tǒng)計(jì)圖;
(3)全年級(jí)有480人,估計(jì)對(duì)錯(cuò)題“全解決”和“大部分解決”共有多少學(xué)生?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半徑為2,圓心角為60°,則圖中陰影部分的面積是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
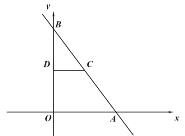
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() 為坐標(biāo)原點(diǎn),直線
為坐標(biāo)原點(diǎn),直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() .
.
(1)求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),以每秒
出發(fā),以每秒![]() 個(gè)單位長(zhǎng)度的速度沿
個(gè)單位長(zhǎng)度的速度沿![]() 勻速運(yùn)動(dòng),同時(shí)點(diǎn)
勻速運(yùn)動(dòng),同時(shí)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),以每秒
出發(fā),以每秒![]() 個(gè)單位長(zhǎng)度的速度沿
個(gè)單位長(zhǎng)度的速度沿![]() 勻速運(yùn)動(dòng),設(shè)點(diǎn)
勻速運(yùn)動(dòng),設(shè)點(diǎn)![]() 運(yùn)動(dòng)的時(shí)間為
運(yùn)動(dòng)的時(shí)間為![]() 秒
秒![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(3)在(2)的條件下,過(guò)點(diǎn)![]() 作
作![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,連接
,連接![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 中點(diǎn),連接
中點(diǎn),連接![]() ,求
,求![]() 為何值時(shí),直線
為何值時(shí),直線![]() 與
與![]() 軸相交所成的銳角與
軸相交所成的銳角與![]() 互余.
互余.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線![]() (m,n 為常數(shù)).
(m,n 為常數(shù)).
(1)若拋物線的的對(duì)稱軸為直線 x=1,且經(jīng)過(guò)點(diǎn)(0,-1),求 m,n 的值;
(2)若拋物線上始終存在不重合的兩點(diǎn)關(guān)于原點(diǎn)對(duì)稱,求 n 的取值范圍;
(3)在(1)的條件下,存在正實(shí)數(shù) a,b( a<b),當(dāng) a≤x≤b 時(shí),恰好有![]() ,請(qǐng)直接寫出 a,b 的值.
,請(qǐng)直接寫出 a,b 的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com